
The minimum force required to move the body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is
(A)
(B)
(C)
(D)
Answer
500.4k+ views
Hint:
- We should know friction.
- We should have knowledge of all the forces acting or a body or air inclined plane.
- We need to know the relation between the frictional force
Complete step by step Solution:
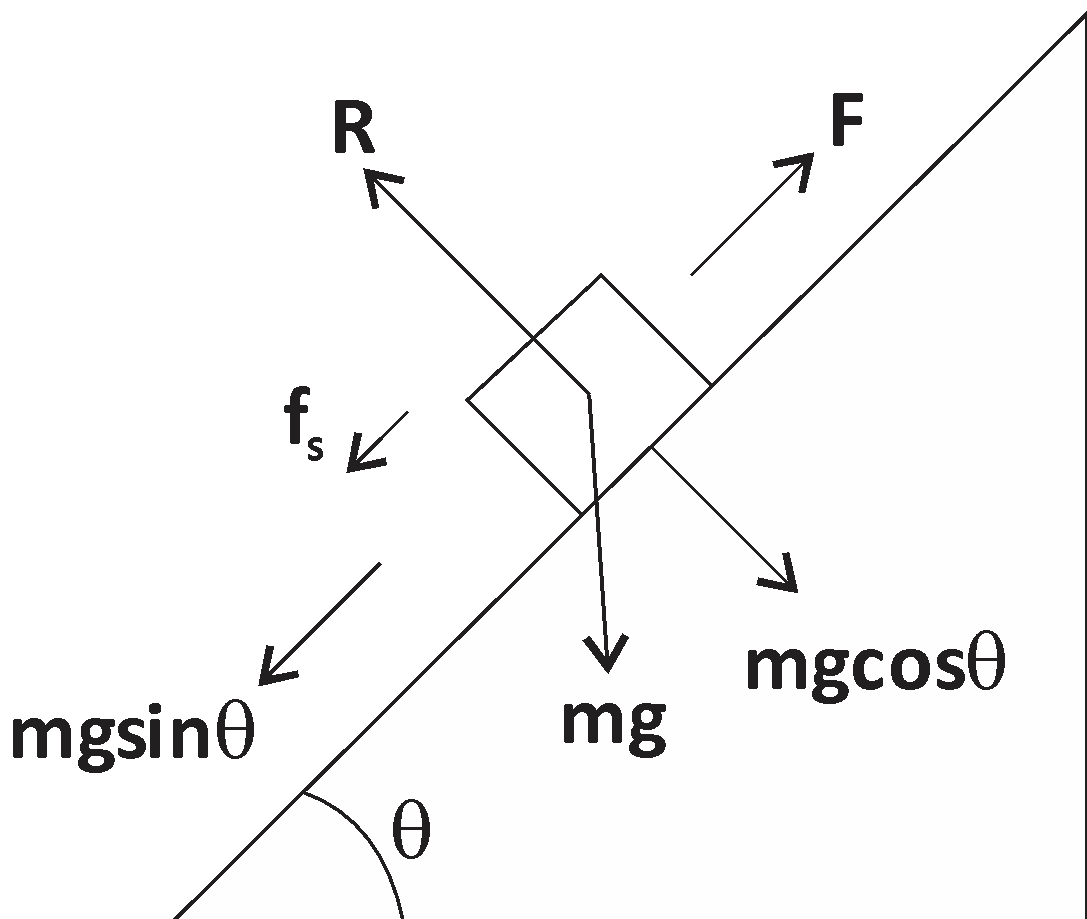
Here, the mass of the body
Applied force
Friction force
Acceleration due to gravity
Angle of the inclined plane
Coefficient of friction
Now, for the body to move up, opposing forces are
For preventing the body opposing force is
Force
Now, given,
Given,
So, option (c) is correct.
Note:
- We to take case while calculating upward 4 downward force
- Fup should be greater than
- We have to take care while calculating numerical value.
- We should know friction.
- We should have knowledge of all the forces acting or a body or air inclined plane.
- We need to know the relation between the frictional force
Complete step by step Solution:

Here, the mass of the body
Applied force
Friction force
Acceleration due to gravity
Angle of the inclined plane
Coefficient of friction
Now, for the body to move up, opposing forces are
For preventing the body opposing force is
Force
Now, given,
Given,
So, option (c) is correct.
Note:
- We to take case while calculating upward 4 downward force
- Fup should be greater than
- We have to take care while calculating numerical value.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




