Question

The minimum value of \[F\] for which the block remains at rest will be –
(A). \[mg(\sin \theta -\mu \cos \theta )\]
 (B). \[mg(\sin \theta +\mu \cos \theta )\]
(C). \[mg(\tan \theta -\mu \sin \theta )\]
(D). \[mg(\cos \theta -\mu \sin \theta )\]

Answer 1

Hint: According to the second law of motion, an external force is required to change the state of rest or motion of a body. Resolve all the forces acting on the block into its components individually for x components and y components of the forces and use the equations to find the minimum value of force.
Formulas Used:
\[F+{{F}_{\mu }}=mg\sin \theta \]
\[N=mg\cos \theta \]
\[{{F}_{\mu }}=\mu N\]

Complete answer:
A block of mass \[m\]is kept on an inclined plane with a coefficient of friction, \[\mu \]. The forces acting on the body are-
 

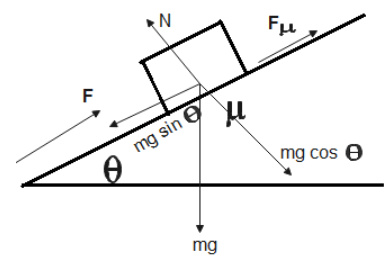
\[mg\] is resolved into its x and y components.
\[\theta \] is the angle of inclination of the slide
 In the x-direction, the forces acting are-
\[F+{{F}_{\mu }}=mg\sin \theta \] - (1)
Here,
\[{{F}_{\mu }}\] is the frictional force
Forces acting in the y-direction,
\[N=mg\cos \theta \] - (2)
Here,\[N\] is the normal force acting between the surfaces in contact
We know that,
\[{{F}_{\mu }}=\mu N\]
Therefore, from eq (2), we get,
\[{{F}_{\mu }}=\mu mg\cos \theta \] - (3)
Substituting eq (3) in eq (1), we get,
\[\begin{align}
  & F+\mu mg\cos \theta =mg\sin \theta \\
 & \therefore F=mg\sin \theta -\mu mg\cos \theta \\
 & \Rightarrow F=mg(\sin \theta -\mu \cos \theta ) \\
\end{align}\]
Therefore, the value of \[F\] for which the block will remain in the position of rest is \[F=mg(\sin \theta -\mu \cos \theta )\].

So, the correct option is (A).

Note:
Normal force is also called contact force. It is exerted by surfaces on each other to prevent them from passing through them. Frictional force is the force that opposes the motion of an object. It occurs due to the locking of irregularities between surfaces. All forces acting on the block are considered internal forces of the system as the system is at rest.