Question

The moment of inertia of a circular ring with mass M and radius R about an axis passing through its centre and perpendicular to its plane is:
A. $\dfrac{MR^2}{4}$
B. $MR^2$
C. $\dfrac{MR^2}{2}$
D. $\dfrac{3}{4}MR^2$

Answer 1

Hint: Begin by first taking a small elementary length over the circumference of the ring. Find the effective mass of this elementary length. Following this, obtain an expression for the moment of inertia of the ring contributed by this elementary mass. Integrate this expression over the entire circumference of the ring to obtain the effective moment of inertia of the circular ring.

Formula used: Moment of inertia $I=MR^2$

Complete step by step answer:
Given that the mass of the ring is M, and the radius of the ring is R, let AB be the axis passing through the centre of the ring that is perpendicular to the plane of the ring as shown in the diagram.
Therefore, AB is at a distance R from the circumference of the ring.
We are now going to determine the moment of inertia of the ring about this axis. For this, let us consider a circumferential length element of the ring dx whose mass element is dm.

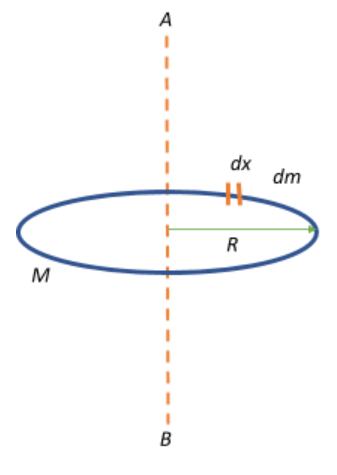
The length of the circular ring or its circumference is given as $2\pi R$
Following this, the mass of the elementary length of the ring will be a fractional mass of the whole ring, i.e.,
$dm = \dfrac{dx}{2\pi R} \times M = \dfrac{M}{2\pi R}.dx$
The moment of inertia of this elementary part of the ring about axis AB is given as:
$dI = dmR^2$
$\Rightarrow dI = \left(\dfrac{M}{2\pi R}dx \right).R^2$
The moment of inertia about the AB axis of the whole ring can be taken over the entire circumference and is given as:
$\Rightarrow I = \int dI = \int_{x=0}^{x=2\pi R} \dfrac{M}{2\pi R}R^2.dx$
$\Rightarrow I = \dfrac{MR}{2\pi}.\int_{x=0}^{x=2\pi R} dx$
$\Rightarrow I = \dfrac{MR}{2\pi}|x|_{0}^{2\pi R} = \dfrac{MR}{2\pi}.2\pi R = MR^2$

So, the correct answer is “Option B”.

Note: Recall that the moment of inertia is dependent on the distribution of mass in the body about the axis of rotation, the position and orientation of the axis of rotation and the shape of the body. Thus, the moment of inertia of the same circular ring would be different if it had a different axis of rotation. For example, if the axis of rotation of was passing through the diameter along the plane of the ring, then the moment of inertia would be $I = \dfrac{MR^2}{2}$, and about a tangent to the circular ring would be $I=\dfrac{3MR^2}{2}$.