Question

The moment of inertia of a hollow cubical box of mass$M$ and side$a$ about an axis passing through the centres of two opposite faces is equal to
A. $\dfrac{{5M{a^2}}}{3}$
B. $\dfrac{{5M{a^2}}}{6}$
C. $\dfrac{{5M{a^2}}}{{12}}$
D. $\dfrac{{5M{a^2}}}{{18}}$

Answer 1

Hint: Consider a hollow cubical box. Find the individual moment of inertia of each face about the centre of mass of the respective faces. Then find the moment of inertia of each face about the axis passing through the centres of any fixed two opposite faces. Apply parallel and perpendicular axis theorems to find the moment of inertia about desired axis.

Complete step by step answer:

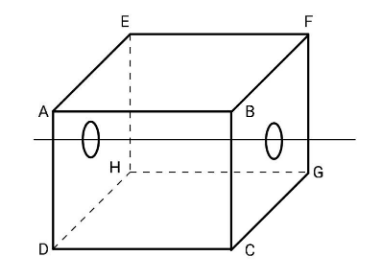
The mass of the whole cube is $M$, since there are six faces, the individual masses of each face will be $m = \dfrac{M}{6}$. Let the axis passing through the center of the faces AEHD and BFGC ne OO’.

Consider the face ABCD:
The moment of inertia of square lamina is given by $I = \dfrac{{m{a^2}}}{6}$. Therefore, ${I_{_0ABCD}} = \dfrac{{m{a^2}}}{6}$ about the centre and perpendicular to the face.
The moment of inertia of ABCD about the axis passing through the centre of ABCD and parallel to the sides AB and BC are equal and will be found out by using the perpendicular axis theorem. The perpendicular axis theorem states that the moment of inertia of a planar lamina about an axis perpendicular to the lamina is equal to the sum of moment of inertias of the lamina about the two perpendicular axes.
So,
 $
I + I = \dfrac{{m{a^2}}}{6} \\
\Rightarrow I = \dfrac{{m{a^2}}}{{12}} \\
$

Now, applying the parallel axis theorem which states that the moment of inertia about an axis is equal to the moment of inertia about a parallel axis passing through the center of mass plus the product of mass of the body and square of the distance between the parallel axes.
Therefore, the moment of inertia of ABCD about OO’ is
\[
{I_{ABCD}} = \dfrac{{m{a^2}}}{{12}} + m{\left( {\dfrac{a}{2}} \right)^2} \\
\Rightarrow {I_{ABCD}} = \dfrac{{m{a^2}}}{3} \\
\]
Due to symmetry, the moment of inertia of EFGH about OO’ will be \[{I_{EFGH}} = \dfrac{{m{a^2}}}{3}\]

Similarly, For faces ABFE and DCGH, the moment of inertia will be the same as above.
Therefore, ${I_{ABFE}} = {I_{DCGH}} = \dfrac{{m{a^2}}}{3}$.
For the faces AEHD and BFGC,
The moment of inertia will be ${I_{AEHD}} = {I_{BFGC}} = \dfrac{{m{a^2}}}{6}$
Now, the total moment of inertia will be the sum of moment of inertia of individual faces.
$
I = {I_{ABCD}} + {I_{EFGH}} + {I_{BFGC}} + {I_{AEHD}} + {I_{DHGC}} + {I_{AEFB}} \\
\Rightarrow I = \dfrac{{m{a^2}}}{3} + \dfrac{{m{a^2}}}{3} + \dfrac{{m{a^2}}}{6} + \dfrac{{m{a^2}}}{6} + \dfrac{{m{a^2}}}{3} + \dfrac{{m{a^2}}}{3} \\
\Rightarrow I = \dfrac{{5m{a^2}}}{3} \\
$
Substituting the value of $m$
$\therefore I = \dfrac{{5M{a^2}}}{{18}}$.
The moment of inertia of a hollow cubical box of mass $M$ and side $a$ about an axis passing through the centres of two opposite faces is equal to $\dfrac{{5M{a^2}}}{{18}}$.

Hence, option D is the correct answer.

Note: Always remember that in the parallel axis theorem, the parallel axis should always pass through the centre of mass of body and the distance $d$ is the perpendicular distance between the desired axis and the parallel axis passing through the centre of mass.