
Answer
390.8k+ views
Hint: Moment of Inertia is the name given to rotational inertia, the rotational analog of mass for straight movement. It shows up in the connections for the dynamics of rotational movement. The moment of inertia must be determined regarding a picked pivot of revolution. For a point mass, the moment of inertia is only the mass multiplied by the square of perpendicular distance to the rotational axis, $I=m{{r}^{2}}$. That point mass relationship turns into the reason for all different moments of inertia since any item can be developed from an assortment of point masses.
Complete step by step answer:
To solve the given question, we must apply the concept of the moment of inertia.
We consider the given diagram to answer the given question,
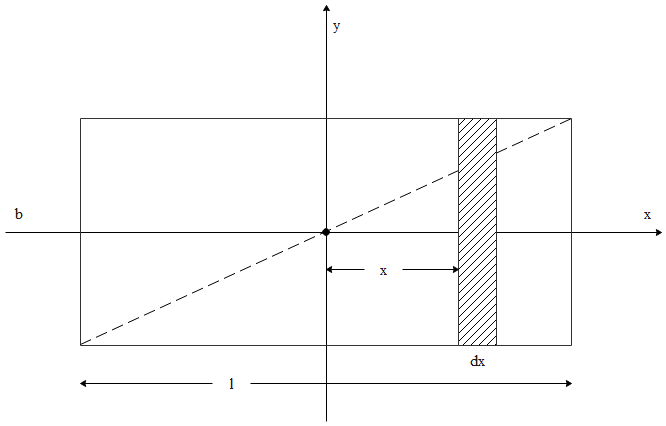
We can calculate the differential area as,
$\Rightarrow d A=b d x$
$\Rightarrow \sigma =\dfrac{M}{l\times b}$
Therefore,
$\Rightarrow dM=\sigma dA\Rightarrow \dfrac{Mdx}{lb}$
Integrating the values, we get,
$\Rightarrow \int{d}{{I}_{y}}=\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{d}M\times {{x}^{2}}$
$\Rightarrow {{I}_{y}}=\dfrac{M}{l}\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{{{x}^{2}}}dx$
$\Rightarrow \dfrac{M{{l}^{2}}}{12}$
Similarly, ${{I}_{y}}=\dfrac{M{{b}^{2}}}{12}$
$\Rightarrow {{I}_{z}}={{I}_{x}}+{{I}_{y}}=\dfrac{M{{b}^{2}}}{12}+\dfrac{M{{l}^{2}}}{12}$
$\Rightarrow M\left( \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \right)$
Therefore, the correct answer is Option A.
Note: Moment of Inertia is characterized as for a particular rotation axis. The moment of inertia of a point mass with deference toward a pivot is characterized as the result of the mass multiplied by the distance from the axis squared. The moment of inertia of any all-inclusive article is developed from that essential definition. The overall type existing apart from the moment of inertia includes an integral.
Complete step by step answer:
To solve the given question, we must apply the concept of the moment of inertia.
We consider the given diagram to answer the given question,

We can calculate the differential area as,
$\Rightarrow d A=b d x$
$\Rightarrow \sigma =\dfrac{M}{l\times b}$
Therefore,
$\Rightarrow dM=\sigma dA\Rightarrow \dfrac{Mdx}{lb}$
Integrating the values, we get,
$\Rightarrow \int{d}{{I}_{y}}=\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{d}M\times {{x}^{2}}$
$\Rightarrow {{I}_{y}}=\dfrac{M}{l}\int\limits_{-\dfrac{l}{2}}^{\dfrac{l}{2}}{{{x}^{2}}}dx$
$\Rightarrow \dfrac{M{{l}^{2}}}{12}$
Similarly, ${{I}_{y}}=\dfrac{M{{b}^{2}}}{12}$
$\Rightarrow {{I}_{z}}={{I}_{x}}+{{I}_{y}}=\dfrac{M{{b}^{2}}}{12}+\dfrac{M{{l}^{2}}}{12}$
$\Rightarrow M\left( \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \right)$
Therefore, the correct answer is Option A.
Note: Moment of Inertia is characterized as for a particular rotation axis. The moment of inertia of a point mass with deference toward a pivot is characterized as the result of the mass multiplied by the distance from the axis squared. The moment of inertia of any all-inclusive article is developed from that essential definition. The overall type existing apart from the moment of inertia includes an integral.
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Name the scale on which the destructive energy of an class 11 physics JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main

Other Pages
A ball of mass 05 Kg moving with a velocity of 2ms class 11 physics JEE_Main

If two bulbs of 25W and 100W rated at 200V are connected class 12 physics JEE_Main

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

A mosquito with 8 legs stands on the water surface class 11 physics JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main



