Question

The moment of inertia of a rod of mass M and length L about an axis passing through on edge of perpendicular to its length will be:
A. \[\dfrac{{M{L^2}}}{{12}}\]
B. \[\dfrac{{M{L^2}}}{6}\]
C. \[\dfrac{{M{L^2}}}{3}\]
D. \[M{L^2}\]

Answer 1

Hint – In this question we need to know the moment of inertia about an axis perpendicular to the rod and then apply parallel and perpendicular theorem, to find the required moment of inertia about the given axis.
Formula used – 1) ${I_C} = \dfrac{{M{L^2}}}{{12}}$
1) Parallel theorem: $I = {I_C} + M{(\dfrac{L}{2})^2}$

Complete step-by-step answer:
Inertia is the measure of resistance that a body of a certain mass offers when plunged into motion or, on the contrary, bought to a halt by an external force. Inertia, or the tendency of objects to resist change, varies with mass. Heavier objects are difficult to accelerate when at rest and equally difficult to stop when in motion, as compared to lighter objects.

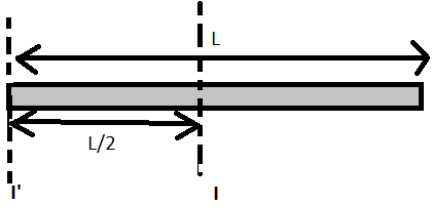
Given,
Length =L
Mass = M
We know that the moment of inertia about an axis perpendicular to the rod and passing through its centre is $\dfrac{{M{L^2}}}{{12}}$. Now we need to M.O.I about an axis through its edge and perpendicular to the rod.
Applying parallel theorem, we get
$
  I' = {I_0} + M{(\dfrac{L}{2})^2} \\
  I' = \dfrac{{M{L^2}}}{{12}} + \dfrac{{M{L^2}}}{4} \\
  I' = \dfrac{{4M{L^2}}}{{12}} = \dfrac{{M{L^2}}}{3} \\
  I' = \dfrac{{M{L^2}}}{3} \\
 $
Hence, the correct option is C.

Note – In this type of question we need to remember their M.O.I. about an axis perpendicular to the object and then we can easily apply parallel and perpendicular theorems to get the desired conditions of the axis. Rotational inertia is significant in almost all physical problems involving mass in rotational motion. It is used to measure angular momentum which helps one to understand (by retaining angular momentum) how rotational motion varies as the distribution of mass changes. Inertia is directly proportional to the body's density. If you're going to feel inertia, then I'd say you drive a car and a paper ball. The car has more mass, and thus more inertia.