Question

The Moment of inertia of a thin semicircular disc (mass = M & radius = R) about an axis through point O and perpendicular to the plane of the disc, is given by:

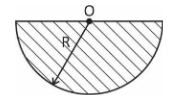
(A) \[\dfrac{1}{4}M{{R}^{2}}\]
(B) \[\dfrac{1}{2}M{{R}^{2}}\]
(C) \[\dfrac{1}{8}M{{R}^{2}}\]
(D) \[M{{R}^{2}}\]

Answer 1

Hint:We know that the Moment of inertia of a disc about an axis passing through its centre of mass and perpendicular to the axis of rotation is given by, \[I=\dfrac{1}{2}M{{R}^{2}}\]. Now knowing this we can easily find the moment of inertia of half disc easily because the axis of rotation does not change.

Complete step by step answer:
We know that the moment of inertia of a whole circle with mass M is
\[I=\dfrac{1}{2}M{{R}^{2}}\].
But in this case, the mass of half of the circle is M.
So, 2M will be the mass of the whole circle.
Therefore, the moment of inertia of the whole of the circle is
\[=2\times I\]
\[=2\times \dfrac{1}{2}M{{R}^{2}}\]
\[=M{{R}^{2}}\]
and then a moment of inertia of half of the circle is half of this value i.e.
\[I=\dfrac{1}{2}M{{R}^{2}}\]
Hence, the correct option is (B)

Note:Moment of inertia of two semicircular discs with the same mass and radius is equal to \[M{{R}^{2}}\]. Also, it can be easily seen that that just mass is half, so we can directly tell the result by using the value of reduced mass. In problems involving moments of inertia it is very important to see what is the axis of rotation and whether it is parallel to it or perpendicular to it. Also, we can use the theorem of parallel axis and theorem of perpendicular axis.