Question

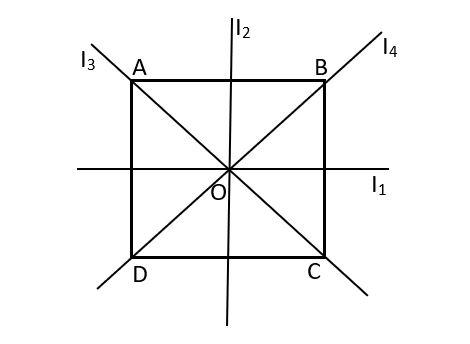
The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is:

A.)${I_1}+{I_2}$
B.)${I_3}+{I_4}$
C.)${I_1}+{I_3}$
D.)${I_1}+{I_2}+{I_3}+{I_4}$

Answer 1

Hint: We will first look for the pair of mutually perpendicular axes among the ones given in the diagram. Then by applying perpendicular axis theorem which states that for a planar lamina, the moment of inertia about an axis perpendicular to the plane is equal to the sum of moments of inertia about the two axes in the plane of the lamina mutually perpendicular to each other and intersecting in the same plane at a point from where the axis perpendicular to the plane passes. With this we will get the required answer.

Complete step by step answer:
Moment of inertia of the square plate ABCD has been given about four of its axes, all into the plane of the sheet viz. ${I_1}, {I_2}, {I_3}$ and ${I_4}$, where $I_2$ and $I_1$, are mutually perpendicular to each other and similarly, ${I_3}$ and $I_4$ are perpendicular to each other.
We need to find the moment of inertia $I$ of the plate about, about an axis passing through the centre O and perpendicular to the plane of the sheet.

From the perpendicular axis theorem, we know that for a planar lamina, the moment of inertia about an axis perpendicular to the plane is equal to the sum of moments of Inertia about the two axes in the plane of the lamina mutually perpendicular to each other and intersecting in the same plane at a point from where the axis perpendicular to the plane passes.

Thus, we can write that $I={I_1}+{I_2}={I_3}+{I_4}$
Or else, $2I= {I_1}+{I_2}+{I_3}+{I_4}$
Hence, options a and b are the correct answers.

Note:
This question has multiple correct answers, so by mistake one may not choose all the answers. Also, by perpendicular axis theorem, we must note that the two axes should be perpendicular to each other and the third axis should be perpendicular to the plane of object and should pass through the point of intersection of the two mutually perpendicular axes.