Question

The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through-

Answer 1

Hint: The moment of inertia of a body is its tendency to resist change which causes rotational motion in it, i.e. the angular acceleration. It is mathematically given as the product of the mass of the body and its radius of gyration. Using the standard expression for moment of inertia of a uniform circular disc, later, we apply parallel axis theorem to it which gives the moment of inertia about all these points and then choose the one with maximum value for the required answer.

Formula Used
Moment of inertia of a circular disc about an axis through its center of mass and perpendicular to the disc:
${I_{cm}} = \dfrac{{M{R^2}}}{2}$, where ${I_{cm}}$ is the moment of inertia about center of mass, M is the mass of the uniform circular disc and R is the radius of the uniform circular disc.

Parallel axis theorem:
$I = {I_{cm}} + M{d^2}$, where I is the moment of inertia about the parallel axis, ${I_{cm}}$ is the moment inertia about the center, M is the mass of the object and d is the distance between the two axes.

Complete step-by-step answer:
We know that the moment of inertia is the ability of a body to resist its rotational motion caused due to the application of torque by resisting the change in its angular acceleration.
For a uniform circular disc this quantity about an axis passing through the center of mass and perpendicular to the disc is:
${I_{cm}} = \dfrac{{M{R^2}}}{2}$, where ${I_{cm}}$ is the moment of inertia about center of mass, M is the mass of the uniform circular disc and R is the radius of the uniform circular disc.

We know that parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its center of mass and the product of its mass and the square of the distance between the two parallel axes.
Mathematically,
$I = {I_{cm}} + M{d^2}$, where I is the moment of inertia about the parallel axis, ${I_{cm}}$ is the moment inertia about the center, M is the mass of the object and d is the distance between the two axes.

Now, for this uniform circular disc, from parallel axis theorem we have,
The moment of inertia about any axis parallel to the axis passing through the center of the mass is:
$I = {I_{cm}} + M{d^2}$
$\Rightarrow I = \dfrac{{M{R^2}}}{2} + M{d^2}$
where symbols have their usual meaning.
Clearly, the moment of inertia I is dependent on the physical quantity d. As d increases, the moment of inertia I increases.
$d \uparrow {\text{ }}I \uparrow $
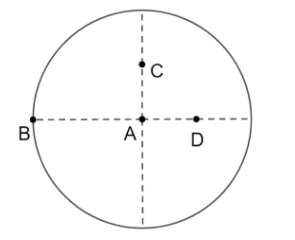
From the above figure, B is the point with the largest distance from the center of mass.
Therefore, the correct answer is B), i.e., the moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through B.

Note: Another way to conclude this question could have been to use the term “proportionality”.
From the given mathematical equation of the moment of inertia about any axis parallel to the axis passing through the center of the mass. It is clear that I is directly proportional to ${d^2}$ .
Mathematically,
$I \propto {d^2}$
So if d increases, ${d^2}$ increases, thus I increase.