Question

The moment of inertia of a uniform solid cone relative to its symmetry axis, if the mass of the cone is equal to $M$ and the radius of its base is to $R$ is $I=\dfrac{3M{{R}^{2}}}{y}$. Find the values of $y$.

Answer 1

Hint: We can find the moment of inertia of the uniform solid cone by finding the moment of inertia of an infinitesimal mass element in the cone and integrating it to find the moment of inertia of the whole cone. Since, the cone is uniform, we can find out a relation between the infinitesimal mass and some other variable of the cone, such as the radius and use this relation in the integration process.

Formula used:
The moment of inertia $I$ of a solid disc of mass $M$ and radius $R$, about an axis perpendicular to its surface and passing through its centre is given by
$I=\dfrac{M{{R}^{2}}}{2}$
Volume $V$ of a cone of radius $R$ and height $H$ is
$V=\dfrac{1}{3}\pi {{R}^{2}}H$

Complete step by step answer:

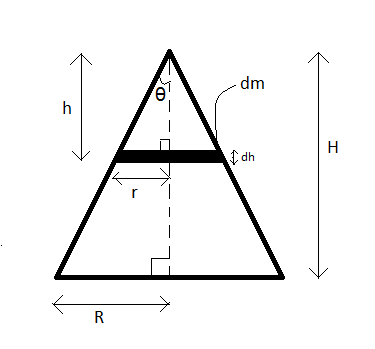
As explained in the hint, we will first find the moment of inertia of an infinitesimal mass element of the uniform cone about the symmetry axis and then integrate it for the whole cone. Also, we will find a relation between the infinitesimal mass element and the radius of the cone which will aid us in the integration process.
Hence, let us proceed to do that by first drawing a figure.

We have a cone of radius $R$, height $H$, semi vertical angle $\theta $ and mass density $\rho $. We take an infinitesimal solid disc element of mass $dm$ at a depth $h$ from the vertex and with radius $r$. The thickness of the disc is $dh$.
Now, volume $V$ of a cone of radius $R$ and height $H$ is
$V=\dfrac{1}{3}\pi {{R}^{2}}H$ --(1)

Therefore, using (1), we get the volume $V$ of the cone is
$V=\dfrac{1}{3}\pi {{R}^{2}}H$
Now, since $\text{Mass = Volume}\times \text{Density}$, we get the mass $M$ of the cone as,
$M=\dfrac{1}{3}\pi {{R}^{2}}H\rho $
$\therefore \rho =\dfrac{3M}{\pi {{R}^{2}}H}$ --(2)
Now, volume $dV$ of the infinitesimal circular thin disc will be its $\text{surface area}\times \text{thickness}$.
$\therefore dV=\pi {{r}^{2}}dh$ $\left( \because \text{Surface area of a circle = }\pi \times \text{radiu}{{\text{s}}^{2}} \right)$
Now, since $\text{Mass = Volume}\times \text{Density}$, we get the mass $dm$ of the infinitesimal disc as,
$dm=\pi {{r}^{2}}dh\rho $ --(3)
Now, from the geometry of the figure, we can observe that,
$\tan \theta =\dfrac{R}{H}=\dfrac{r}{h}$
$\therefore r=\dfrac{R}{H}h$ --(4)
Now, the moment of inertia $I$ of a solid disc of mass $M$ and radius $R$, about an axis perpendicular to its surface and passing through its centre is given by
$I=\dfrac{M{{R}^{2}}}{2}$ --(5)
Hence, using (5), we get the moment of inertia $dI$ of the infinitesimal solid disc element about the symmetry axis (dotted line shown in the figure) as
$dI=dm\dfrac{{{r}^{2}}}{2}$
$\therefore dI=\pi {{r}^{2}}dh\rho \dfrac{{{r}^{2}}}{2}=\dfrac{\pi \rho {{r}^{4}}}{2}dh$ [Using (3)]
$\therefore dI=\dfrac{\pi \rho }{2}{{\left( \dfrac{R}{H}h \right)}^{4}}dh=\dfrac{\pi \rho }{2}\dfrac{{{R}^{4}}}{{{H}^{4}}}{{h}^{4}}dh$ --[Using (4)] --(6)
Now, we will integrate this for the whole cone. Therefore integrating both sides of equation (6) with the respective variable, we get,
$\int\limits_{0}^{I}{dI}=\int\limits_{0}^{H}{\dfrac{\pi \rho }{2}\dfrac{{{R}^{4}}}{{{H}^{4}}}{{h}^{4}}dh}$
$\therefore \left[ I \right]_{0}^{I}=\dfrac{\pi \rho {{R}^{4}}}{2{{H}^{4}}}\int\limits_{0}^{H}{{{h}^{4}}dh}=\dfrac{\pi \rho {{R}^{4}}}{2{{H}^{4}}}\left[ \dfrac{{{h}^{5}}}{5} \right]_{0}^{H}$ $\left( \because \int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}} \right)$
$\therefore \left[ I-0 \right]=\dfrac{\pi \rho {{R}^{4}}}{2{{H}^{4}}}\left[ \dfrac{{{H}^{5}}}{5}-\dfrac{0}{5} \right]=\dfrac{\pi \rho {{R}^{4}}}{2{{H}^{4}}}\left[ \dfrac{{{H}^{5}}}{5} \right]=\dfrac{\pi \rho {{R}^{4}}H}{10}$
$\therefore I=\dfrac{\pi {{R}^{4}}H}{10}\times \dfrac{3M}{\pi {{R}^{2}}H}=\dfrac{3M{{R}^{2}}}{10}$
Hence, the moment of inertia of a uniform solid cone about its symmetric axis is $\dfrac{3M{{R}^{2}}}{10}$.
Now comparing the value with $\dfrac{3M{{R}^{2}}}{y}$, we get,
$\dfrac{3M{{R}^{2}}}{y}=\dfrac{3M{{R}^{2}}}{10}$
$\therefore y=10$
Therefore, the value of $y$ is $10$.

Note: This is the most general method of finding the moment of inertia of a uniform body. However, this is only applicable for a uniform body since we can find out a relation between two different variables of the body (such as the radius and height) that is maintained throughout the whole body. For irregular and non-uniform bodies, there is no such relation and the moment of inertia has to be found out by a series of integration processes.
Students must be adept at this process of considering an infinitesimal mass element, finding out its moment of inertia and extending it for the whole body. However, it should also be mentioned that students should keep in mind the moment of inertia of some common shapes such as a sphere, cone, cube, etc, about some common axes, so that they can solve rotational mechanics’ numerical problems easily. This would save a lot of time especially in competitive examinations where saving time is a priority.