
The moment of inertia of a uniform solid sphere about its diameter is
Answer
503.7k+ views
Hint: To find the moment of inertia of any shape about an unknown axis, first we need to know the moment of inertia of the shape about an axis either perpendicular to it or parallel to it. If we know the moment of inertia of a shape about an axis passing through the centre of mass of the body, then we can find the moment of inertia about any axis parallel to it by the use of parallel axis theorem.
Formula used:
Where M is the mass of the body and d is the distance of the axis from the centre of mass ( COM ) of the body.
Complete step by step answer:
Since every diameter of a sphere passes through its centre of mass, hence the moment of inertia of a sphere about its diameter is also the moment of inertia about its centre of mass. Now, to find the moment of inertia about its tangent, the distance between diameter and a tangent equals ‘R’.
Given,
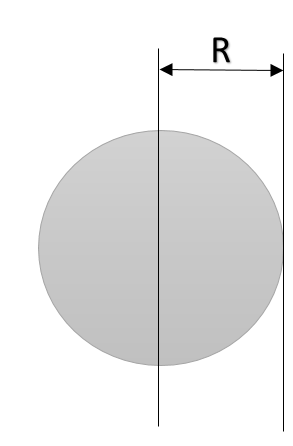
Now using parallel axis theorem:
As we know, the moment of inertia of solid sphere about its an axis passing through its centre of mass
is
Hence
Or
Now putting
So, the correct answer is “Option D”.
Note:
While using the Parallel axis theorem, one axis should always be the one passing through the centre of mass. Chance of mistakes is high if one avoids this information. Students are advised to learn the moment of inertia of commonly used shapes for example: Disc, sphere, etc.
Formula used:
Where M is the mass of the body and d is the distance of the axis from the centre of mass ( COM ) of the body.
Complete step by step answer:
Since every diameter of a sphere passes through its centre of mass, hence the moment of inertia of a sphere about its diameter is also the moment of inertia about its centre of mass. Now, to find the moment of inertia about its tangent, the distance between diameter and a tangent equals ‘R’.
Given,

Now using parallel axis theorem:
As we know, the moment of inertia of solid sphere about its an axis passing through its centre of mass
is
Hence
Or
Now putting
So, the correct answer is “Option D”.
Note:
While using the Parallel axis theorem, one axis should always be the one passing through the centre of mass. Chance of mistakes is high if one avoids this information. Students are advised to learn the moment of inertia of commonly used shapes for example: Disc, sphere, etc.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




