Question

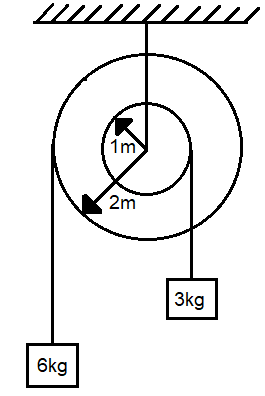
The moment of inertia of the pulley system as shown in the figure is $3kg - {m^2}$. The radii of the bigger and smaller pulleys are 2m and 1m respectively. As the system is released from rest, find the angular acceleration of the pulley system (Assume that there is no slipping between string & pulley and string is light) [Take $g = 10m/{s^2}$]

Answer 1

Hint
From the figure, we can determine the free body diagrams for both the blocks and find the free body equations for both the cases. From there we find the expressions for the tensions in both the strings. By substituting these tensions in the torque equations and writing the linear accelerations in terms of the angular accelerations we get the value of the angular acceleration.
In the solution to this question we will be using the following formula,
From the free-body diagrams,
$\Rightarrow F - T = ma$
Where $F$ is the force and $T$ is the tension on the string.
and the torque equation,
$\Rightarrow {T_1}{r_1} - {T_2}{r_2} = I\alpha $
Where ${T_1}$ and ${T_2}$ are the tensions in the two strings, $\Rightarrow {r_1}$ and ${r_2}$ are the radius of the two pulleys.
$I$ is the moment of inertia and $\alpha $ is the angular acceleration of the system.

Complete step by step answer
In this question, we are given a pulley system consisting of two pulleys and 2 masses.
let the mass of the bigger block be $M = 6kg$
and mass of the smaller block, $m = 3kg$
The radius of the bigger pulley is ${r_1} = 2m$
and the radius of the smaller pulley is ${r_2} = 1m$
So we can redraw the figure as,

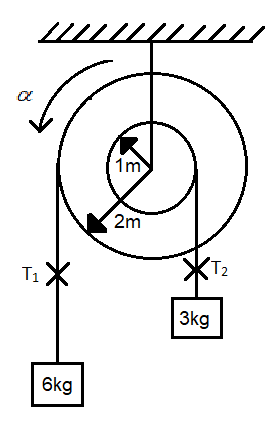
Now we draw the free body diagram of the blocks as follows,

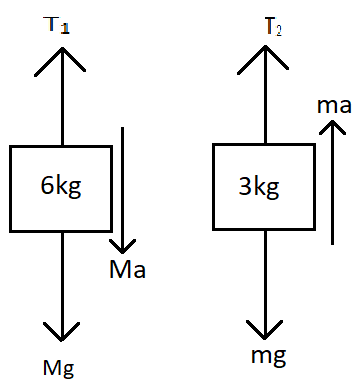
From the free-body diagrams, we get the equations of motion of the pulleys as,
$\Rightarrow Mg - {T_1} = Ma$ for the bigger block
Therefore, we can find the expression of ${T_1}$ as,
$\Rightarrow {T_1} = Mg - Ma$and,
$\Rightarrow {T_2} - mg = ma$ for the smaller block
From here we can find the expression of ${T_2}$ as,
$\Rightarrow {T_2} = mg + ma$
Now for the pulley, the torque equation is given by,
$\Rightarrow {T_1}{r_1} - {T_2}{r_2} = I\alpha $
Here we can substitute the expressions of the tensions as,
$\Rightarrow \left( {Mg - Ma} \right){r_1} - \left( {mg + ma} \right){r_2} = I\alpha $
Here $a$ is the linear accelerations of the blocks. So we can write the linear acceleration in terms of the angular acceleration as,
$\Rightarrow a = {r_1}\alpha $ for the bigger block and $a = {r_2}\alpha $ for the smaller block. Therefore substituting we get,
$\Rightarrow \left[ {Mg - M\left( {{r_1}\alpha } \right)} \right]{r_1} - \left[ {mg + m\left( {{r_2}\alpha } \right)} \right]{r_2} = I\alpha $
Now substituting the values of the masses and the radii we get,
$\Rightarrow \left[ {6g - 6\left( {2\alpha } \right)} \right]2 - \left[ {3g + 3\left( \alpha \right)} \right] = I\alpha $
On opening the brackets we get,
$\Rightarrow 12g - 24\alpha - 3g - 3\alpha = I\alpha $
In the question, the value of the moment of inertia of the pulley system is given, $I = 3kg - {m^2}$.
Substituting this value we get,
$\Rightarrow 12g - 24\alpha - 3g - 3\alpha = 3\alpha $
taking $\alpha $ common we have,
$\Rightarrow 12g - 3g = 3\alpha + 24\alpha + 3\alpha $
$ \Rightarrow 9g = 30\alpha $
Therefore the value of angular acceleration is,
$\Rightarrow \alpha = \dfrac{{9g}}{{30}}$
Putting the value of $g = 10m/{s^2}$
$\Rightarrow \alpha = \dfrac{{9 \times 10}}{{30}} = 3rad/{s^2}$
So the angular acceleration of the system is $\alpha = 3rad/{s^2}$.

Note
The moment of inertia is the rotational equivalent of the mass in linear motion. It is the tendency of the body to resist angular acceleration. It is calculated by the sum of the product of the masses of each particle and their distance from the axis of rotation.