
The motion of a pendulum is an example of:
A. Translatory motion
B. Rotational motion
C. Oscillatory motion
D. Curvilinear motion
Answer
496.2k+ views
Hint: A motion in which a particle undergoes periodic motion is called Simple harmonic motion (S.H.M). Not every periodic motion is S.H.M but every S.H.M is periodic motion. The revolution of earth about the sun is an example of periodic motion but it is not simple harmonic. A motion is said to be simple harmonic only if the acceleration of the particle is the function of first power of displacement and having direction opposite of the displacement.
Complete answer:
Mathematically we can say that if the motion is simple harmonic, it must follow the standard differential equation of simple harmonic motion which is given by
Let’s now displace the bob by a small angle
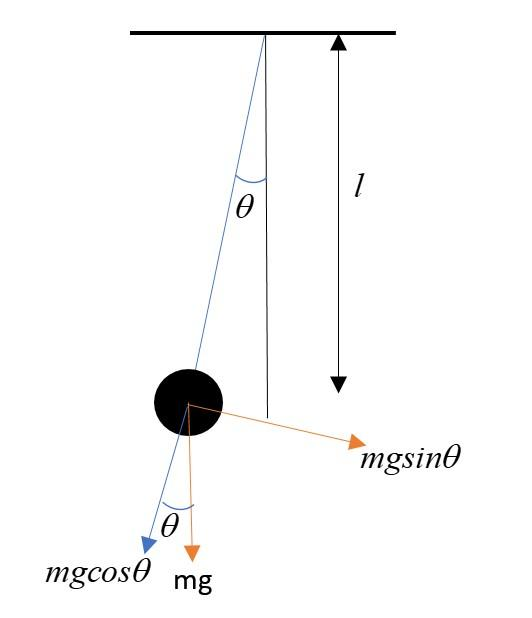
After taking components of the weight, we can see that the only force responsible for the restoring motion of the pendulum is
Or
For smaller angles,
Thus,
Now, we know that
Also,
So
Which is the equation of S.H.M. Thus the given motion is simple harmonic. Since simple harmonic motion is an oscillatory motion.
So, the correct answer is “Option C”.
Note:
Students can make mistakes about the fact that every simple harmonic motion is periodic but not every periodic motion is simple harmonic. The revolution of a fan about its own axis is an example of simple harmonic motion. On comparing the obtained equation with the equation of S.H.M, we get a time period of a simple pendulum is
Complete answer:
Mathematically we can say that if the motion is simple harmonic, it must follow the standard differential equation of simple harmonic motion which is given by

Let’s now displace the bob by a small angle

After taking components of the weight, we can see that the only force responsible for the restoring motion of the pendulum is
Or
For smaller angles,
Thus,
Now, we know that
Also,
So
Which is the equation of S.H.M. Thus the given motion is simple harmonic. Since simple harmonic motion is an oscillatory motion.
So, the correct answer is “Option C”.
Note:
Students can make mistakes about the fact that every simple harmonic motion is periodic but not every periodic motion is simple harmonic. The revolution of a fan about its own axis is an example of simple harmonic motion. On comparing the obtained equation with the equation of S.H.M, we get a time period of a simple pendulum is
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




