Question

The near point and far point of a person are 40 cm and 250 cm respectively.
Determine the power of the lens he/she should use while reading a book kept at a distance 25 cm from the eye.
A. 2.5 D
B. 5.0 D
C. 1.5 D
D. 3.5 D

Answer 1

Hint: The person will be able to read the book if its image can be formed at 40 cm from his eyes. But the book is at a distance of 25 cm. So, we need a converging lens (convex) of appropriate focal length. It can be better understood from the diagram.

Formula used:
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$

Complete step-by-step solution:

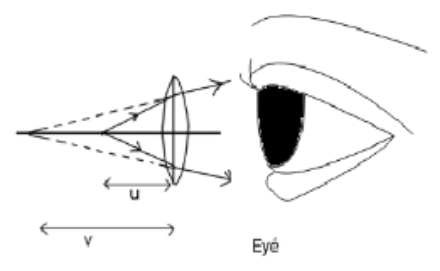
The image distance must be $v = -40cm$. The negative sign is due to the fact that it is measured in the opposite of the direction of light. The object distance is clearly $u=-25 cm$. So, from the lens formula,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Taking LCM, we get
$\dfrac{u-v}{vu}=\dfrac{1}{f}$
Taking reciprocal and substituting the values, we get
$\begin{align}
& f=\dfrac{uv}{u-v} \\
& \Rightarrow f=\dfrac{(-40)(-25)}{(-25)-(-40)} \\
& \Rightarrow f=\dfrac{1000}{15} \\
& \Rightarrow f=\dfrac{200}{3}cm \\
\end{align}$
$f=\dfrac{2}{3} m$
Power of the lens is,
$P=\dfrac{1}{f}=\dfrac{3}{2}=1.5D$
Hence option C is the correct answer.

Additional information:
When a person cannot see objects that are very close to him but can see the things that are far away, the problem or defect is called Hypermetropia. In this condition, the person has to use a convex lens. When a person can’t see things that are away from him but can see things close to him, the problem is called Myopia. It’s treated by using a concave lens. In both cases, virtual images are formed by the lenses.

Note: Take good care of the sign convention. Usually in case of virtual images, both the image and the object are on the same side of the lens. To avoid mistakes, notice that power is given in Diopter when the focal length is given in meters. The power is always positive for convex lenses and negative for concave lenses.