Question

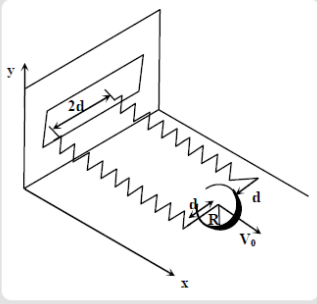
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is

 \[
  {\mathbf{A}}.\;\;\;{\mathbf{kx}} \\
 {\mathbf{B}}.\;\;\;\;{\mathbf{2}}{\text{ }}{\mathbf{kx}} \\
 {\mathbf{C}}.\;\;\;\dfrac{{{\mathbf{2}}{\text{ }}{\mathbf{kx}}}}{{\mathbf{3}}} \\
 {\mathbf{D}}.\;\;\;\;\dfrac{{{\mathbf{4}}{\text{ }}{\mathbf{kx}}}}{{\mathbf{3}}} \\
\]

Answer 1

Hint: Net Force acting on a body is given by the formula:
\[{\vec F_{Net}} = m.\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \]
Where,
\[{\vec F_{Net}}\] is the net force acting on the body
m is the mass of the body
\[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \] is the acceleration of the body
Moment of Force is called Torque.
Net Torque acting on a body is given by the formula,
\[{\vec \tau _{Net}} = I\vec \alpha \]
Where,
\[{\vec \tau _{Net}}\] is the net Torque acting on the body
I is the moment of inertia of the body
\[\vec \alpha \]is the angular acceleration of the body
Also,
\[{\vec \tau _{Net}} = \vec F \times R\]
Moment of inertia of a disk is given by the formula,
$I = \dfrac{1}{2}M{R^2}$

Using all the above formulas, we can easily compute the result.

Complete step by step solution: Net Force acting on a body is given by the formula:
\[{\vec F_{Net}} = m.\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \]
Where,
\[{\vec F_{Net}}\] is the net force acting on the body
m is the mass of the body
\[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {a} \] is the acceleration of the body
We will insert \[( - 2kx + F)\]in the place of \[{\vec F_{Net}}\]
\[ - 2kx + F = M{a_c}\] Equation 1
Where,
k is the spring constant
x is the distance by which the spring has been stretched
F is the friction force on the disk
M is the mass of disk
\[{a_c}\] is the acceleration of centre of mass of the disk
Net Torque acting on a body is given by the formula,
\[{\vec \tau _{Net}} = I\vec \alpha \] Equation 2
Where,
\[{\vec \tau _{Net}}\] is the net Torque acting on the body
I is the moment of inertia of the body
\[\vec \alpha \]is the angular acceleration of the body
Additionally, Torque is also calculated as follows,
\[{\vec \tau _{Net}} = \vec F \times R\] Equation 3
Where,
R is the distance of the Force from the centre of mass of the body

Now combining equations 2 and 3,
We get,
$\vec F \times R = I\vec \alpha $
$\vec F = \dfrac{{I\vec \alpha }}{R}$ Equation 4
In Pure Rolling condition,
\[{a_c} = {\vec \alpha _c}R\]
Moment of inertia of a disk is given by the formula,
$I = \dfrac{1}{2}M{R^2}$
Inserting the values of $\alpha $ and I in equation 4,
We get,
\[F = \dfrac{{\dfrac{1}{2}M{R^2}}}{R} \times \dfrac{{{a_c}}}{R}\]
$ = > F = \dfrac{1}{2}M{a_c}$
Inserting the value of F in equation 1,
We get,
$ = > - 2kx + \dfrac{1}{2}M{a_c} = - M{a_c}$
$ = > \dfrac{1}{2}M{a_c} + M{a_c} = 2kx$
$ = > \dfrac{3}{2}M{a_c} = 2kx$
$ = > M{a_c} = \dfrac{4}{3}kx$
$ = > M{a_c} = - \dfrac{4}{3}kx$

Hence, Option (D) is correct.

Note:
We have used a negative sign because the disk has been displaced away from the equilibrium position. Hence this force will tend to bring the disk back to its initial position.