
The normal chord at a point t on the parabola
(a) 4
(b) 2
(c) 1
(d) 3
Answer
516.9k+ views
Hint: Assume that the chord is normal to the parabola at point P whose coordinate is given as
Complete step-by-step solution -
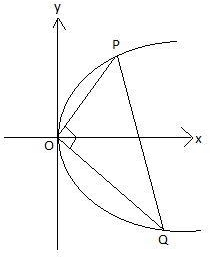
We know that, if two lines are perpendicular to each other then the product of their slopes is equal to
Slope of line OP
Slope of line OQ
Taking the product of slopes, we get,
Now, since PQ is a normal to the parabola and the general equation of a parabola is
Since, the line PQ passes through
Substituting m = -t in the above equation, we get,
Therefore, ‘-t’ is the slope of line PQ.
Also, slope of the line PQ
Cancelling the common terms, we get,
Slope of line PQ
Therefore, equating (-t) with
Substituting the value of
Hence, option (b) is the correct answer.
Note: One may note that the equation of normal to the parabola is a cubic equation in ‘m’ that means a total of three normal can be drawn from a point outside the parabola. We have used a hit and trial method to determine one of the values of ‘m’ in terms of ‘t’. The other two values of ‘m’ are of no use here because we are already getting a simplified relation between t and
Complete step-by-step solution -

We know that, if two lines are perpendicular to each other then the product of their slopes is equal to
Slope of line OP
Slope of line OQ
Taking the product of slopes, we get,
Now, since PQ is a normal to the parabola and the general equation of a parabola is
Since, the line PQ passes through
Substituting m = -t in the above equation, we get,
Therefore, ‘-t’ is the slope of line PQ.
Also, slope of the line PQ
Cancelling the common terms, we get,
Slope of line PQ
Therefore, equating (-t) with
Substituting the value of
Hence, option (b) is the correct answer.
Note: One may note that the equation of normal to the parabola is a cubic equation in ‘m’ that means a total of three normal can be drawn from a point outside the parabola. We have used a hit and trial method to determine one of the values of ‘m’ in terms of ‘t’. The other two values of ‘m’ are of no use here because we are already getting a simplified relation between t and
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




