Question

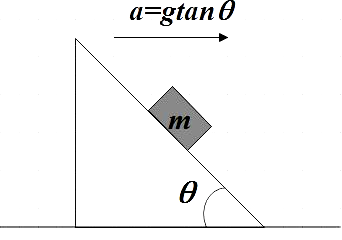
The normal force acting on block in the situation shown is N. If all the surfaces are smooth, the value of N is

A. $mg\cos \theta $
B. $\dfrac{mg}{\cos \theta }$
C. $mg\sin \theta $
D. $\dfrac{mg}{\sin \theta }$

Answer 1

Hint: Make the free body diagram of the body of mass m. Mark the normal force and other forces acting on the body and also resolve these forces into its components. Then, you could balance the forces in the same direction. If you don’t miss out any force while making the free body diagram, you will get the Normal force correctly.

Complete answer:
In the question we are given an inclined plane with an inclination $\theta $ and this inclined plane is accelerating with an acceleration of $a=g\tan \theta $
We also have a body of mass m that is kept on the inclined plane. Let us assume that this body is sliding without slipping. We are also said that all surfaces are smooth which implies that there is no friction between the mass m and the inclined also not between the inclined plane and ground. If N is the normal force acting on the mass m, we are asked to find which among the given options gives the expression for this normal force.

In questions like this, all you have to do is make a free body diagram for all the given masses as a first step.

This figure may appear a bit messy so let us give a description on it.
So, basically all we have done is that we have resolved the forces acting on the mass m into its components.
We have a normal force acting on the body N and we have resolved this into its components as $N\cos \theta $ and $N\sin \theta $
Then we have the weight of the body acting downward and also we have force due to the acceleration of the inclined plane and we have also resolved both of them.
Now let us balance the forces acting along the y-axis,
$mg=N\cos \theta $
$\Rightarrow N=\dfrac{mg}{\cos \theta }$
Therefore, we get the expression for normal force as,
$N=\dfrac{mg}{\cos \theta }$

So, the correct answer is “Option B”.

Note:
In case you wish to find N directly, you could equate the forces in that direction as,
$\Rightarrow N=mg\cos \theta +ma\sin \theta $
But $a=g\tan \theta $
$\Rightarrow N=mg\cos \theta +mg\tan \theta \sin \theta =mg\left( \cos \theta +\dfrac{{{\sin }^{2}}\theta }{\cos \theta } \right)$
$\Rightarrow N=mg\left( \dfrac{{{\cos }^{2}}\theta +{{\sin }^{2}}\theta }{\cos \theta } \right)=\dfrac{mg}{\cos \theta }$
We see that we get the same expression for N.
You could also equate $N\sin \theta =ma=mg\tan \theta $ to find the same.
Most important point is that, while making the free body diagram, take care that you don’t miss any of the forces. A perfect FBD assures the correct answer.