
The number of real circle cutting orthogonally the circle
(a) 0
(b) 1
(c) 2
(d) Infinitely many
Answer
509.7k+ views
Hint: To solve the given question, we will use the fact that if two circles are orthogonal, then the tangents at intersection point will have an angle of
Complete step by step solution:
Before we solve the question, we must know what orthogonal of circles is. Two circles
Now, we will assume that,
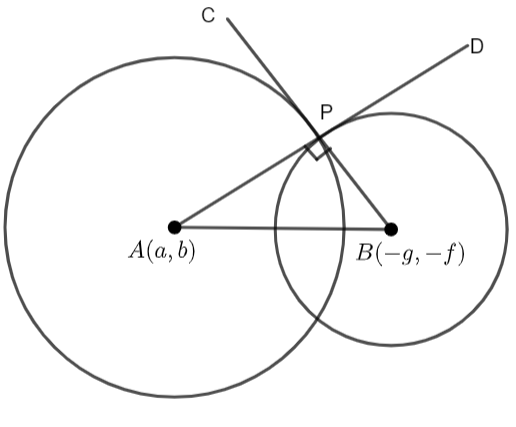
Now, the two circles are orthogonal if the tangents AD and BC are at right angles. So, the angle between the tangents AD and BC is
Now, we will find the values of ‘a’ and ‘b’. ‘a’ is the x – coordinate of the centre of
Similarly,
Therefore, the centre of
Now, we can see that PAB is a right-angled triangle. So, here we will apply the Pythagoras theorem. The Pythagoras theorem states that, in a right-angled triangle, if H is the hypotenuse, R is the perpendicular and J is the base, then we have,
In our case, H = AB, R = AP and J = BP. Thus, we have,
Here, AP and BP are the radii of the circles
Now, AB is calculated with the help of the distance formula. The distance formula is given by,
where
Now, we will put the values of AB, AP and BP from (iv), (ii) and (iii) to (i). Thus, we will get,
Here, we can see that there are infinite values of g, f and c that satisfy the above relation. So, we will have infinite circles which are orthogonal to the given circle.
Hence, option (d) is the right answer.
Note: The alternate method of solving the question is if the two circles
In our case,
We will replace g by x, f by y and c by z and we get,
The above equation is an equation of the plane which contains infinite points. So, there are infinite values of x, y and x. Hence, there are infinite orthogonal circles.
Complete step by step solution:
Before we solve the question, we must know what orthogonal of circles is. Two circles
Now, we will assume that,

Now, the two circles are orthogonal if the tangents AD and BC are at right angles. So, the angle between the tangents AD and BC is
Now, we will find the values of ‘a’ and ‘b’. ‘a’ is the x – coordinate of the centre of
Similarly,
Therefore, the centre of
Now, we can see that PAB is a right-angled triangle. So, here we will apply the Pythagoras theorem. The Pythagoras theorem states that, in a right-angled triangle, if H is the hypotenuse, R is the perpendicular and J is the base, then we have,
In our case, H = AB, R = AP and J = BP. Thus, we have,
Here, AP and BP are the radii of the circles
Now, AB is calculated with the help of the distance formula. The distance formula is given by,
where
Now, we will put the values of AB, AP and BP from (iv), (ii) and (iii) to (i). Thus, we will get,
Here, we can see that there are infinite values of g, f and c that satisfy the above relation. So, we will have infinite circles which are orthogonal to the given circle.
Hence, option (d) is the right answer.
Note: The alternate method of solving the question is if the two circles
In our case,
We will replace g by x, f by y and c by z and we get,
The above equation is an equation of the plane which contains infinite points. So, there are infinite values of x, y and x. Hence, there are infinite orthogonal circles.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




