Question

The number of vibrational degrees of freedom for a $C{{O}_{2}}$ molecule is
a) 4
b) 5
c) 6
d) 9

Answer 1

Hint: Though carbon dioxide is a triatomic molecule, it is not arranged in a triangular fashion. It is a linear molecule with all the three atoms arranged in the same line. Hence we would use the relation between the number of linkages of the atoms of the molecule to determine the vibrational degrees of freedom for a $C{{O}_{2}}$.

Complete step-by-step answer:
Let us first understand what does degrees of freedom in a molecule means,
Degrees of freedom of a system or a molecule is the number of independent ways in which the particles of the system can absorb energy.
It can also be defined as the number of coordinates required to specify the position of the constituent particles of the system minus the number of independent relation, i.e.
$f=3N-k$ where f is the degrees of freedom, N is the number of particles in the system and k is the independent relation between the particles.
The above relation that we obtained is for total degrees of freedom of a molecule at moderate temperatures. But at higher temperatures the molecule possesses an additional degree of freedom that is a vibrational degree of freedom. Hence, now the number of degrees of freedom of a molecule with N particles is given by,
$f=\text{Translational + Rotational + Vibrational}...(1)$. The total number of degrees of freedom for a linear molecule is given by 3N, where N is the no of atoms of the molecule. For a linear carbon dioxide molecule, it has 3 translational and 2 rotational degrees of freedom hence the equation 1 becomes,
$\begin{align}
  & f=3+2+\text{Vibrational} \\
 & \text{Vibrational}=3N-5 \\
\end{align}$
A $C{{O}_{2}}$molecule has 3 atoms, two of oxygen and one carbon atom. Hence the vibrational degrees of freedom of the molecule is,
$\begin{align}
  & \text{Vibrational}=3N-5 \\
 & \text{Vibrational}=3(3)-5 \\
 & \text{Vibrational}=9-5=4 \\
\end{align}$
Hence the carbon dioxide molecule has 4 vibrational degrees of freedom. Hence the correct answer is option a.


Note:

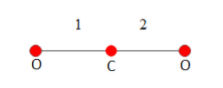
In a symmetric carbon dioxide molecule as shown above, the two oxygen molecules vibrate about the carbon molecule. Each vibrational motion has both kinetic and potential energies. So one degree of freedom of vibrational motion is taken as two. Since the above molecule vibrates along two linkages we can directly conclude it has four degrees of freedom.