Question

The number of zeroes of the polynomial from the graph is

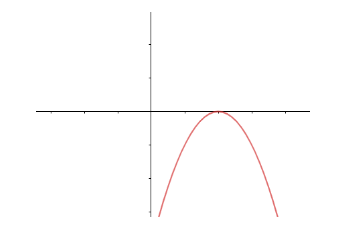
(a) 0
(b) 1
(c) 2
(d) 3

Answer 1

Hint: Start drawing all the details about the equation of the curve that you can gather from the graph given. The given is a parabola, so, the equation of the curve is a quadratic equation, so can have a maximum of two roots. Also, it is touching the x-axis, i.e., meeting the x-axis at only one point, so it has repeated roots. So, use all these details to reach the answer.

Complete step-by-step answer:
Let us start the solution to the above question by drawing the graph given in the question.

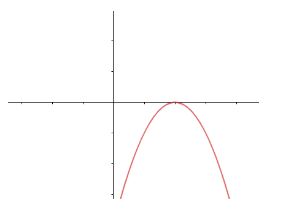
The curve given in the question is a parabola. For example: A general parabola with vertex at (0,0) can be represented by the equation $ {{x}^{2}}=4ay $ , which is a polynomial in which the maximum power of x is 2, so it is a quadratic equation. So, it is a sure thing that the equation of the curve is a quadratic equation. As it is a quadratic equation, the degree of the equation is 2, so it can have a maximum of two roots.
Also, the graph is touching the x-axis at a single point and the number of points where a curve cuts the x-axis is the number of roots of the equation of the curve. So, the given curve has one repeated root, i.e., only one root.
Hence, the answer to the above question is option (b).

Note: The other things that we can get after looking at the curve in the graph is: the coefficient of $ {{x}^{2}} $ in the equation of the curve is negative as the parabola is opening downward. Also, the root of the equation is positive, as the graph meets the x-axis in the right of the origin. The range of the equation of the curve is $ (-\infty ,0] $ .