Question

The opposite angles of a parallelogram are (3x-2) and (x+48). Find the measure of each angle of the parallelogram.

Answer 1

Hint: We know the property of a parallelogram that opposite angles of a parallelogram are equal to each other. And it is given that opposite angles of the parallelogram are (3x-2) and (x+48). We also know the property that the sum of adjacent angles of a parallelogram is equal to \[{{180}^{0}}\] . Put the value of x in (3x-2) and get its measure. Now, using this angle, get the measure of adjacent angles.

Complete step-by-step answer:

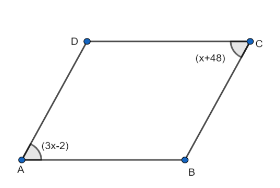
We have a parallelogram ABCD whose opposite angles are (3x-2) and (x+48).
We know the property of a parallelogram that the measure of opposite angles is equal to each other.
Here, \[\angle DAB\] and \[\angle BCD\] are opposite to each other. So, as per the above property, we can say that \[\angle DAB\] and \[\angle BCD\] are equal to each other.
\[\angle DAB\] = \[\angle BCD\] …………………(1)
According to the question, it is given that the opposite angles are (3x-2) and (x+48).
Let us assume,
\[\angle DAB=\left( 3x-2 \right)\] ………………(2)
\[\angle BCD=\left( x+48 \right)\] …………….(3)
From equation (1), equation (2), and equation (3), we get
\[\left( 3x-2 \right)=\left( x+48 \right)\]
\[\begin{align}
  & \Rightarrow 3x-x=48+2 \\
 & \Rightarrow 2x=50 \\
 & \Rightarrow x=25 \\
\end{align}\]
Now, putting the value of x in equation (2) and equation (3), we get
\[\angle DAB={{\left( 3x-2 \right)}^{0}}={{(3.25-2)}^{0}}={{73}^{0}}\] ……………….(4)
 \[\angle BCD={{\left( x+48 \right)}^{0}}={{(25+48)}^{0}}={{73}^{0}}\] ………………..(5)
We also know the property of a parallelogram that the sum of adjacent angles of a parallelogram is equal to \[{{180}^{0}}\] .
Here, the angle \[\angle ADC\] is adjacent to \[\angle DAB\] . So, as per the above property, we can say that the sum of the \[\angle ADC\] and \[\angle DAB\] is equal to \[{{180}^{0}}\] .
\[\angle ADC+\angle DAB={{180}^{0}}\] ……………..(5)
From equation (4) and equation (5), we get
\[\angle ADC+\angle DAB={{180}^{0}}\]
\[\begin{align}
  & \Rightarrow \angle ADC+{{73}^{0}}={{180}^{0}} \\
 & \Rightarrow \angle ADC={{180}^{0}}-{{73}^{0}} \\
\end{align}\]
\[\Rightarrow \angle ADC={{107}^{0}}\] …………………….(6)
We have the property that in a parallelogram the measure of opposite angles is equal to each other.
Here, \[\angle ADC\]and \[\angle ABC\] are opposite to each other. So, as per the above property, we can say that \[\angle ADC\] and \[\angle ABC\] are equal to each other.
\[\angle ADC=\angle ABC\] ……………………(7)
From equation (6) and equation (7), we have
\[\angle ADC=\angle ABC={{107}^{0}}\] ………………..(8)
From equation (4), equation (5), and equation (8), we have
\[\angle DAB={{73}^{0}}\] , \[\angle BCD={{73}^{0}}\] , and \[\angle ADC=\angle ABC={{107}^{0}}\] .
Hence, the angles are \[{{73}^{0}}\] , \[{{107}^{0}}\] , \[{{73}^{0}}\] , and \[{{107}^{0}}\] .

Note: In this question, one might do a mistake in the property. One can think that the sum of the opposite angles of a parallelogram is equal to \[{{180}^{0}}\] . Also, one can think that the measure of the adjacent angles is equal which is wrong. So, we have to keep the properties of the parallelogram in mind.