Question

The orthocenter, circumcenter, centroid, and incenter of the triangle formed by the line \[y=x+a\] with the coordinate axes lie on
(A) \[{{x}^{2}}+{{y}^{2}}=1\]
(B) \[y=x\]
(C) \[y=2x\]
(D) \[y=3x\]

Answer 1

Hint: First of all, draw the graph of the straight line \[y=x+a\] . We have to find the orthocenter, circumcenter, centroid, and incenter of \[\Delta OAB\] . Now, with the help of the graph get the coordinates of the points O, A, and B. We know the property that the orthocenter of a right-angled triangle lies on the vertex having \[90{}^\circ \] . Now, get the orthocenter. We know the property that the diameter of the circumcircle lies on the hypotenuse of the right-angled triangle and get the coordinate of the circumcenter by using the formula \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] . We know the formula to find the coordinates of the centroid of the triangle, \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] . Use this formula and the coordinate of the centroid. Use Pythagoras theorem and get the hypotenuse. Now, use the formula \[\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\] and get the coordinate of the incenter. Now, solve further and get the curve on which the orthocenter, circumcenter, centroid, and incenter of the triangle lie.

Complete step-by-step answer:
According to the question, it is given that a triangle is being formed by the line \[y=x+a\] with coordinate axes. We have to find the equation of the curve where the orthocenter, circumcenter, centroid, and incenter of the triangle is lying.
First of all, we have to plot the graph of the straight line, \[y+x=a\] ……………(1)

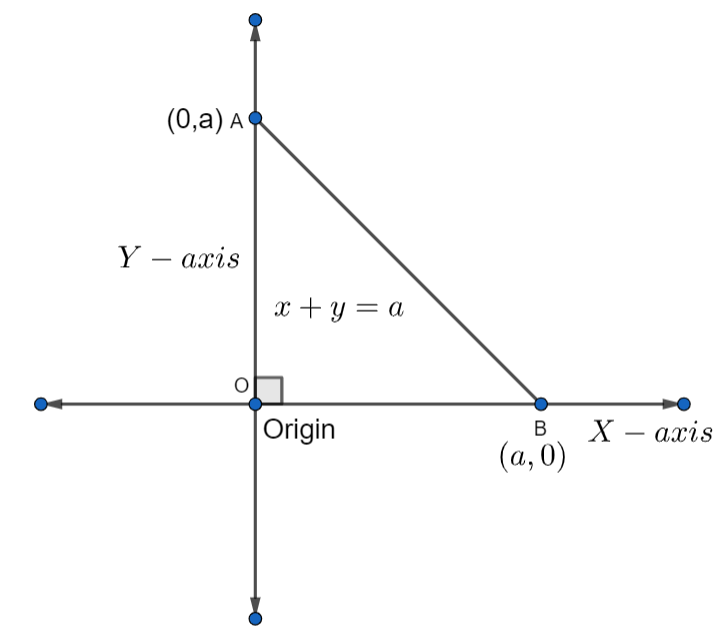
From equation (1), we have the equation of the straight line, \[y+x=a\] .
Transforming equation (1), we get
\[\begin{align}
  & y+x=a \\
 & \Rightarrow \dfrac{y}{a}+\dfrac{x}{a}=1 \\
\end{align}\]
So, the x-intercept and y-intercept of the straight line \[y+x=a\] are equal to a.
The coordinate of the point where the line \[\left( y+x=a \right)\] intersects x-axis = \[\left( a,0 \right)\] .
The coordinate of the point where the line \[\left( y+x=a \right)\] intersects y-axis = \[\left( 0,a \right)\] .
For \[\Delta OAB\] , we have three vertex and the coordinates of the vertex are
O = \[\left( 0,0 \right)\] ………………(2)
A= \[\left( 0,a \right)\] ………………….(3)
B= \[\left( a,0 \right)\] ……………………(4)
Now, we have to find the orthocenter, circumcenter, centroid, and incenter.
In the \[\Delta OAB\] , we have \[\angle AOB\] which is equal to \[90{}^\circ \] . It means \[\Delta OAB\] is a right-angled triangle and we know the property that the orthocenter of a right-angled triangle lies on the vertex having \[90{}^\circ \] . In \[\Delta OAB\] , we have vertex O which has \[90{}^\circ \] . So, the orthocenter of \[\Delta OAB\] lie on the vertex O.
From equation (2), we have the coordinate of the vertex O.
The coordinate of the orthocenter of the \[\Delta OAB\] = \[\left( 0,0 \right)\] ………………..(5)
We know the property that the diameter of the circumcircle lies on the hypotenuse of the right-angled triangle.
So, the side AB is the diameter of the circumcircle and the midpoint of AB is the circumcenter of \[\Delta OAB\] .
We know the formula for the coordinates of the midpoint between two points, \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] ………………….(6)
Here, using this formula to find the midpoint of the side AB.
From equation (3) and equation (4), we have the coordinates of the points A and B.
Now, putting the coordinates of point A and point B in equation (6), we get
\[\left( \dfrac{0+a}{2},\dfrac{a+0}{2} \right)=\left( \dfrac{a}{2},\dfrac{a}{2} \right)\]
The coordinate of the circumcenter of the \[\Delta OAB\] = \[\left( \dfrac{a}{2},\dfrac{a}{2} \right)\] ………………………….(7)
We know the formula to find the coordinates of the centroid of the triangle, \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] ………………………..(8)
From equation (2), equation (3) and equation (4), we have the coordinates of the points O, A, and B.
Now, putting the coordinates of the point O, A, and point B in equation (8), we get
\[\left( \dfrac{0+0+a}{3},\dfrac{0+a+0}{3} \right)=\left( \dfrac{a}{3},\dfrac{a}{3} \right)\]
The coordinate of the centroid of the \[\Delta OAB\] = \[\left( \dfrac{a}{3},\dfrac{a}{3} \right)\] …………………….(9)
In \[\Delta OAB\] , we have
OA = a
OB = a
Here, OA is the height, OB is the base and AB is the hypotenuse of the \[\Delta OAB\] .
Now, using Pythagoras theorem
\[\begin{align}
  & {{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Height \right)}^{2}} \\
 & \Rightarrow A{{B}^{2}}=O{{B}^{2}}+O{{A}^{2}} \\
 & \Rightarrow A{{B}^{2}}={{a}^{2}}+{{a}^{2}} \\
 & \Rightarrow A{{B}^{2}}=2{{a}^{2}} \\
 & \Rightarrow AB=\sqrt{2}a \\
\end{align}\]
We know the formula to find the coordinates of incenter of a triangle,
\[\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\] …………………(10)
Here, a, b, and c are the lengths of the sides of the triangle.
We have to find the incenter of the \[\Delta OAB\] .
In \[\Delta OAB\] , the lengths of the sides are \[a,a,\sqrt{2}a\] .
From equation (2), equation (3) and equation (4), we have the coordinates of the points O, A, and B.
Now, putting the coordinates of the point O, A, and point B in equation (11), we get
\[\begin{align}
  & \left( \dfrac{\sqrt{2}a.0+a.0+a.a}{a+a+\sqrt{2}a},\dfrac{\sqrt{2}a.0+a.a+a.0}{a+a+\sqrt{2}a} \right) \\
 & =\left( \dfrac{a.a}{2a+\sqrt{2}a},\dfrac{a.a}{2a+\sqrt{2}a} \right) \\
 & =\left( \dfrac{{{a}^{2}}}{2a+\sqrt{2}a},\dfrac{{{a}^{2}}}{2a+\sqrt{2}a} \right) \\
\end{align}\]
The coordinate of the incenter of the \[\Delta OAB\] = \[\left( \dfrac{{{a}^{2}}}{2a+\sqrt{2}a},\dfrac{{{a}^{2}}}{2a+\sqrt{2}a} \right)\] ………………(11)
From equation (5), equation (7), equation (9), and equation (11), we have the coordinates of the orthocenter, circumcenter, centroid, and incenter of \[\Delta OAB\] .
The coordinate of the orthocenter of the \[\Delta OAB\] = \[\left( 0,0 \right)\] .
The coordinate of the circumcenter of the \[\Delta OAB\] = \[\left( \dfrac{a}{2},\dfrac{a}{2} \right)\] .
The coordinate of the centroid of the \[\Delta OAB\] = \[\left( \dfrac{a}{3},\dfrac{a}{3} \right)\] .
The coordinate of the incenter of the \[\Delta OAB\] = \[\left( \dfrac{{{a}^{2}}}{2a+\sqrt{2}a},\dfrac{{{a}^{2}}}{2a+\sqrt{2}a} \right)\] .
We can see that the x-coordinates of these points are equal to the y-coordinates of these points.
So, \[y=x\] is the straight line where the orthocenter, circumcenter, centroid, and incenter lies.
Hence, the correct option is (B).

Note: In this question, we can also use section formula to get the coordinates of the circumcenter.
We know the property that the centroid divides the line joining the orthocenter and circumcenter in the ratio 2:1.
The coordinate of the orthocenter of the \[\Delta OAB\] = \[\left( 0,0 \right)\] .
The coordinate of the centroid of the \[\Delta OAB\] = \[\left( \dfrac{a}{3},\dfrac{a}{3} \right)\] .
We know the section formula, the coordinate of the point dividing a line in the ratio m:n is,
\[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] ……………………………(1)
Here, we have,
m:n = 2:1 ………………(2)
\[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)\] ……………………(3)
\[\left( {{x}_{2}},{{y}_{2}} \right)=\left( \dfrac{a}{3},\dfrac{a}{3} \right)\] ……………………….(4)
Let the coordinate of the circumcenter be \[\left( x,y \right)\] .

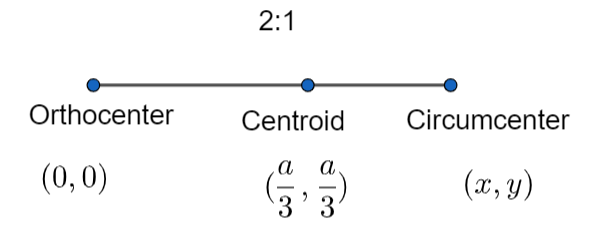
Now, from equation (1), equation (2), equation (3), and equation (4), we get
\[\begin{align}
  & \left( \dfrac{a}{3},\dfrac{a}{3} \right)=\left( \dfrac{2x+1.0}{2+1},\dfrac{2y+1.0}{2+1} \right) \\
 & \Rightarrow \left( \dfrac{a}{3},\dfrac{a}{3} \right)=\left( \dfrac{2x}{3},\dfrac{2y}{3} \right) \\
\end{align}\]
On comparing LHS and RHS we get,
\[\dfrac{a}{3}=\dfrac{2x}{3}\] …………………….(5)
\[\dfrac{a}{3}=\dfrac{2y}{3}\] ………………………(6)
Solving equation (5), we get
\[\begin{align}
  & \dfrac{a}{3}=\dfrac{2x}{3} \\
 & \Rightarrow a=2x \\
 & \Rightarrow \dfrac{a}{2}=x \\
\end{align}\]
 Solving equation (6), we get
\[\begin{align}
  & \dfrac{a}{3}=\dfrac{2y}{3} \\
 & \Rightarrow a=2y \\
 & \Rightarrow \dfrac{a}{2}=y \\
\end{align}\]
Hence, the coordinate of the circumcenter of the \[\Delta OAB\] = \[\left( \dfrac{a}{2},\dfrac{a}{2} \right)\] .