
The orthocenter of an obtuse angled triangle lies_ _ _ _ _ .
Answer
526.8k+ views
Hint-In this question, we use the concept of orthocenter of triangle. The orthocenter of a triangle is the intersection of the three altitudes of a triangle. Remember, the altitude of a triangle is a perpendicular segment from the vertex of the triangle to the opposite side.
Complete step-by-step solution -
Suppose we have an obtuse triangle
Now, we know the orthocenter of a triangle varies with the different types of triangles.
So, we create the altitude from each vertex of the triangle and observe where the all three altitudes meet.
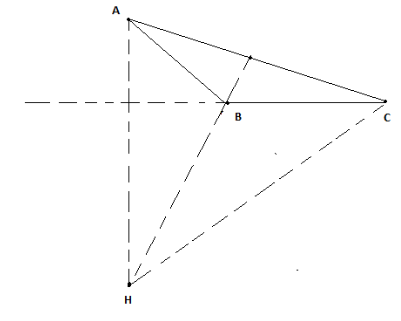
Now, all three altitudes meet at a point H.
The point H is an orthocenter of triangle
We can see that the orthocenter is now outside the triangle because two out of the three altitudes cannot be drawn inside the triangle.
So, the correct option is (a).
Note-In such types of questions we have to find the locus of orthocenter by using the geometrical interpretation because locus of the orthocenter varies from different types of triangles. So, we would always keep in mind that in obtuse triangles orthocenter lie outside the triangle.
Complete step-by-step solution -
Suppose we have an obtuse triangle
Now, we know the orthocenter of a triangle varies with the different types of triangles.
So, we create the altitude from each vertex of the triangle and observe where the all three altitudes meet.

Now, all three altitudes meet at a point H.
The point H is an orthocenter of triangle
We can see that the orthocenter is now outside the triangle because two out of the three altitudes cannot be drawn inside the triangle.
So, the correct option is (a).
Note-In such types of questions we have to find the locus of orthocenter by using the geometrical interpretation because locus of the orthocenter varies from different types of triangles. So, we would always keep in mind that in obtuse triangles orthocenter lie outside the triangle.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




