Question

The orthocenter of the triangle whose vertices are (0, 0), (0, 3), (4, 0) is:
(a) \[\left( 3,\dfrac{7}{3} \right)\]
(b) \[\left( 3,\dfrac{5}{4} \right)\]
(c) \[\left( 5,-2 \right)\]
(d) \[\left( 0,0 \right)\]

Answer 1

Hint: To solve this question, we should know that the orthocenter is nothing but the point of intersection of the triangle’s three altitudes. So, to find the point of intersection of the altitudes we will find the slope of the altitudes of the triangle and then we will find the equation of the altitudes and then their point of intersection.

Complete step-by-step answer:
In this question, we have been asked to find the coordinates of the orthocenter of the triangle with vertices (0, 0), (0, 3) and (4, 0). Let the points be A (0, 0), B (0, 3) and C (4, 0). Now, we will use the formula of the slope, that is
\[Slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
where \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are any two points coordinates of which we find the slope. So, we can write,
The slope of AB = \[\dfrac{3-0}{0-0}=\infty \]
The slope of AC = \[\dfrac{0-0}{4-0}=0\]
The slope of BC = \[\dfrac{3-0}{0-4}=\dfrac{-3}{4}\]
Now, we will use the formula \[{{m}_{1}}.{{m}_{2}}=-1\] (if \[{{m}_{1}}\] and \[{{m}_{2}}\] are perpendicular) to find the altitudes of AB, BC, and AC. So, we get,
The slope of altitude of AB = \[\dfrac{-1}{\infty }=0\]
The slope of altitude of AC = \[\dfrac{-1}{0}=\infty \]
The slope of altitude of BC = \[\dfrac{+4}{3}\]
Now, we know that the altitude on any side of the triangle passes from the opposite vertices like the altitude on BC will pass from A and altitude on AC will pass from B and altitude on AB will pass from C.

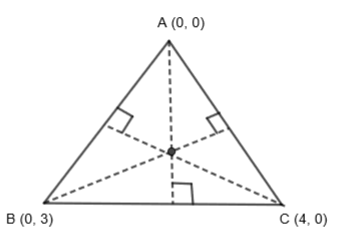
So, we can write the equation of the altitudes by using the slope point formula, that is for point \[\left( {{x}_{1}},{{y}_{1}} \right)\] and slope \[{{m}_{1}}\] it is:
\[y-{{y}_{1}}={{m}_{1}}\left( x-{{x}_{1}} \right)\]
So, we get the equation of the altitude of side AB having the slope as 0 and passes through C as
\[y-0=0\left( x-4 \right)\]
\[\Rightarrow y=0....\left( i \right)\]
And we can write the equation of the altitude of the side BC having a slope \[\dfrac{4}{3}\] and passes through A as
\[y-0=\dfrac{4}{3}\left( x-0 \right)\]
\[3y=4x....\left( ii \right)\]
Now, to find the orthocenter of the triangle, we will find the point of intersection of two equations of the altitudes of two sides. So, we will put the value of y from equation (i) to equation (ii), so we will get,
\[3\left( 0 \right)=4x\]
x = 0
Hence, the coordinates of the orthocenter is (0, 0), which is point A.

Note: We can also solve this question by forming the actual diagram of the triangle by placing the point on the graph.

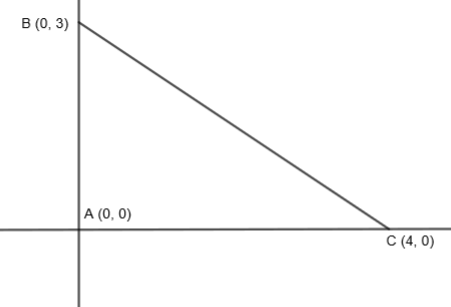
We know that both the axis are perpendicular to each other, so these three coordinates will form a right-angled triangle, with right-angle at A. And we know that the right-angled triangles have orthocenter at the point where the right angle is formed, that is point A (0, 0).