
Answer
432.6k+ views
Hint: Orthocenter of a triangle is defined as the point where perpendiculars drawn from the vertices to the opposite side will intersect each other. For a right-angled triangle, the orthocenter lies at the vertex containing the right angle.
Step By Step Solution:
Let us assume the points as
A = $\left( {{x_1},{y_1}} \right)$ = $\left( {2,\dfrac{{\sqrt 3 - 1}}{2}} \right)$
B = $\left( {{x_2},{y_2}} \right)$ = $\left( {\dfrac{1}{2},\dfrac{{ - 1}}{2}} \right)$
C = $\left( {{x_3},{y_3}} \right)$ = $\left( {2,\dfrac{{ - 1}}{2}} \right)$
Firstly, we calculate the slope of the line AC using the formula,
Slope of AC = $\dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}}$
$\Rightarrow$ Slope of AC = $\dfrac{{\dfrac{{ - 1}}{2} - \left( {\dfrac{{\sqrt 3 - 1}}{2}} \right)}}{{2 - 2}}$
$\Rightarrow$ Slope of AC = $\infty$
As slope of the line is infinity, the line AC will be perpendicular to the X-axis
Then we calculate the slope of the line BC using the formula
Slope of BC = $\dfrac{{{y_3} - {y_2}}}{{{x_3} - {x_2}}}$
$\Rightarrow$ Slope of BC = $\dfrac{{\dfrac{{ - 1}}{2} - \left( {\dfrac{{ - 1}}{2}} \right)}}{{2 - \dfrac{1}{2}}}$
$\Rightarrow$ Slope of BC = 0
As the slope of the line is equal to zero, the line BC will be parallel to X-axis.
Therefore $\Delta ABC$ will be a right angle triangle with $C = 90^\circ$
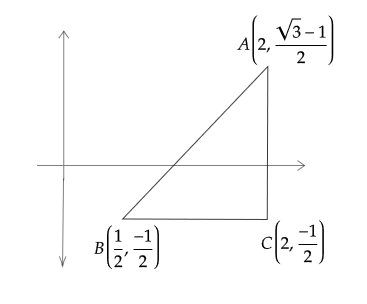
For a right-angled triangle, the orthocenter will be the vertex having an angle of 90 degrees.
$\therefore$ The point $\left( {2,\dfrac{{ - 1}}{2}} \right)$ will be the orthocenter of the
triangle formed by the given vertices.
Therefore the correct answer is Option (B)
Note:
After finding the lines with slope equal to infinity and slope equal to zero, the common point from both the lines should be selected as the vertex containing the right angle. In the above calculation, the slope of AC is infinite and the slope of BC is zero. So point C is selected as a vertex having the right angle.
Step By Step Solution:
Let us assume the points as
A = $\left( {{x_1},{y_1}} \right)$ = $\left( {2,\dfrac{{\sqrt 3 - 1}}{2}} \right)$
B = $\left( {{x_2},{y_2}} \right)$ = $\left( {\dfrac{1}{2},\dfrac{{ - 1}}{2}} \right)$
C = $\left( {{x_3},{y_3}} \right)$ = $\left( {2,\dfrac{{ - 1}}{2}} \right)$
Firstly, we calculate the slope of the line AC using the formula,
Slope of AC = $\dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}}$
$\Rightarrow$ Slope of AC = $\dfrac{{\dfrac{{ - 1}}{2} - \left( {\dfrac{{\sqrt 3 - 1}}{2}} \right)}}{{2 - 2}}$
$\Rightarrow$ Slope of AC = $\infty$
As slope of the line is infinity, the line AC will be perpendicular to the X-axis
Then we calculate the slope of the line BC using the formula
Slope of BC = $\dfrac{{{y_3} - {y_2}}}{{{x_3} - {x_2}}}$
$\Rightarrow$ Slope of BC = $\dfrac{{\dfrac{{ - 1}}{2} - \left( {\dfrac{{ - 1}}{2}} \right)}}{{2 - \dfrac{1}{2}}}$
$\Rightarrow$ Slope of BC = 0
As the slope of the line is equal to zero, the line BC will be parallel to X-axis.
Therefore $\Delta ABC$ will be a right angle triangle with $C = 90^\circ$

For a right-angled triangle, the orthocenter will be the vertex having an angle of 90 degrees.
$\therefore$ The point $\left( {2,\dfrac{{ - 1}}{2}} \right)$ will be the orthocenter of the
triangle formed by the given vertices.
Therefore the correct answer is Option (B)
Note:
After finding the lines with slope equal to infinity and slope equal to zero, the common point from both the lines should be selected as the vertex containing the right angle. In the above calculation, the slope of AC is infinite and the slope of BC is zero. So point C is selected as a vertex having the right angle.
Recently Updated Pages
What is the maximum resistance which can be made using class 10 physics CBSE

Arrange the following elements in the order of their class 10 chemistry CBSE

In the following figure the value of resistor to be class 10 physics CBSE

The magnetic induction at point P which is at a distance class 10 physics CBSE

According to Mendeleevs Periodic Law the elements were class 10 chemistry CBSE

On the portion of the straight line x + 2y 4 intercepted class 11 maths JEE_Main

Trending doubts
Name five important trees found in the tropical evergreen class 10 social studies CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Change the following sentences into negative and interrogative class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

Discuss the main reasons for poverty in India




