Question

The parabola \[{x^2} = {\text{ }}py\] passes through \[\left( {12,{\text{ }}16} \right)\] Then the focal distance of the point is.

Answer 1

Hint: To solve this question, we will start with finding the value of p, then on putting the value of points \[\left( {12,{\text{ }}16} \right)\]in \[{x^2} = {\text{ }}py\], since the parabola passes through the given points. Now after getting the value of p, we will equate both, the given parabola and the standard parabola form., here we will get the value of a. Then afterwards using all the information which we have collected, we will draw the parabola graph and then solve accordingly.

Complete step-by-step answer:
We have been given a parabola \[{x^2} = {\text{ }}py\] which passes through point \[\left( {12,{\text{ }}16} \right).\] We need to find the focal distance of the point \[\left( {12,{\text{ }}16} \right).\]
Since, parabola \[{x^2} = {\text{ }}py\] passes through \[\left( {12,{\text{ }}16} \right),\] then it should satisfy the given points.
Now on putting \[\left( {12,{\text{ }}16} \right)\] in \[{x^2} = {\text{ }}py,\]we get
\[\left( {12} \right){\left( {12} \right)^{}} = {\text{ }}p{\text{ }}\left( {16} \right)\]
\[\Rightarrow p\]$ = \dfrac{{16}}{{12 \times 12}} = 9$
So, we get, \[{x^2} = {\text{ 9}}y\]
Now on comparing above equation with the standard form of parabola, \[{x^2} = {\text{ }}4ay,\]we get
\[\begin{array}{*{20}{l}}
\Rightarrow {{x^2}{\text{ - }}4ay = {x^2}{\text{ - 9}}y} \\
\Rightarrow {4a{\text{ }} = {\text{ }}9}
\end{array}\]
So, we get \[a\]$ = \dfrac{9}{4}$
On drawing graph of the equation, \[{x^2} = {\text{ }}9y,\] we get

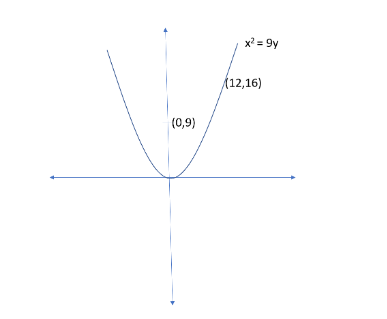
Now, from the figure we get that we need to find the distance from \[\left( {0,9/4} \right)\] to \[\left( {12,16} \right).\]
We will find the focal distance using distance formula, which is
Distance formula $ = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
Let the distance be q, so using distance formula mentioned above, we get
\[\Rightarrow q\]$ = \sqrt {{{(12 - 0)}^2} + {{(\dfrac{9}{4} - 16)}^2}} $
\[\Rightarrow q\]$ = \sqrt {144 + \dfrac{{3025}}{{16}}} = \sqrt {\dfrac{{5329}}{{16}}} $
\[\Rightarrow q\]$ = \dfrac{{73}}{4}$
So, the focal distance of the point is \[\dfrac{{73}}{4}.\]

Note: In the question, we are asked about the focal distance of the point. Focal length is the distance between the vertex and focus, it is measured along the focus of symmetry. That’s why in the question we have found the distance between \[\left( {0,9} \right)\] and \[\left( {12,16} \right).\]