
The parallel sides of trapezium are 6cm and 8cm. If the distance between them is 4cm, its area is
A.28 sq.cm
B.24 sq.cm
C.82 sq.cm
D.42 sq.cm
Answer
479.4k+ views
Hint: In this question, we need to evaluate the area of the trapezium such that the parallel sides of trapezium are 6 cm and 8 cm. For this, we will use the relation between area, length of the parallel sides and length between the parallel sides.
Complete step-by-step answer:
Given the length of the parallel sides of trapezium
The distance between the parallel sides
Let us first draw a trapezium from the above given data
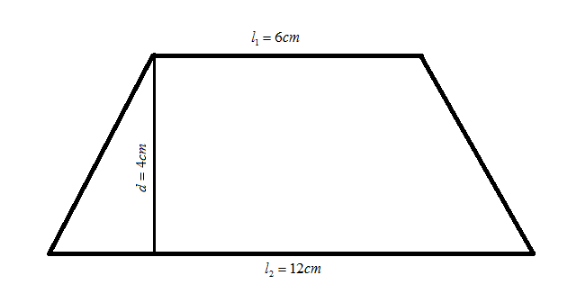
Now we already know the formula for the area of the trapezium which is equal to the product of the sum of parallel sides and distance between them multiplied by half as
Hence, the area of trapezoid whose parallel sides are 6cm and 8cm and the distance between them is 4 cm is
Option A is correct.
So, the correct answer is “Option A”.
Note: When a trapezoid has non parallel sides then the figure is known as irregular trapezoid then to find the area of the trapezoid we divide that geometric figure into a regular triangles or rectangles to find the area of the figure. The area of a trapezium is equal to the product of the sum of the parallel sides and the distance between them multiplied by the half which is given as
Complete step-by-step answer:
Given the length of the parallel sides of trapezium
The distance between the parallel sides
Let us first draw a trapezium from the above given data

Now we already know the formula for the area of the trapezium which is equal to the product of the sum of parallel sides and distance between them multiplied by half as
Hence, the area of trapezoid whose parallel sides are 6cm and 8cm and the distance between them is 4 cm is
Option A is correct.
So, the correct answer is “Option A”.
Note: When a trapezoid has non parallel sides then the figure is known as irregular trapezoid then to find the area of the trapezoid we divide that geometric figure into a regular triangles or rectangles to find the area of the figure. The area of a trapezium is equal to the product of the sum of the parallel sides and the distance between them multiplied by the half which is given as
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

How many ten lakhs are in one crore-class-8-maths-CBSE




