Question

The perimeter of a regular nonagon is 72 meters. Find the area of the polygon in square meters?

Answer 1

Hint: In the above question, we are given a nonagon whose perimeter is given as 72 meters. A polygon which has 9 sides is called a nonagon. The perimeter of the nonagon is given in meters and we have to find the area of the nonagon in square meters. In order to approach the solution, first we have to find the length of each side and then the distance of each edge from the centre of the nonagon. After that we can find the area of each triangle, formed inside the nonagon after joining the centre to the edges. Thus, the area of the nonagon can be obtained.

Complete step-by-step answer:
Given that, the perimeter of the nonagon is
\[ = 72m\]
Since a nonagon has \[9\] sides, hence length of each side is
\[ = \dfrac{{72}}{9}\]
i.e.
\[ = 8m\]
Now join all the \[9\] edges to the centre of the nonagon, in that way \[9\] isosceles triangles will be formed inside the nonagon which divide it into \[9\] equal parts.
Let the distance from the centre to the edges be \[r\] .
Now, the vertical angles of each isosceles triangle will be equal to
\[ = \dfrac{{360^\circ }}{9}\]
i.e.
\[ = 40^\circ \]
Therefore, the other two angles will each be equal to
\[ = \dfrac{{180 - 40^\circ }}{2}\]
i.e.
\[ = 70^\circ \]

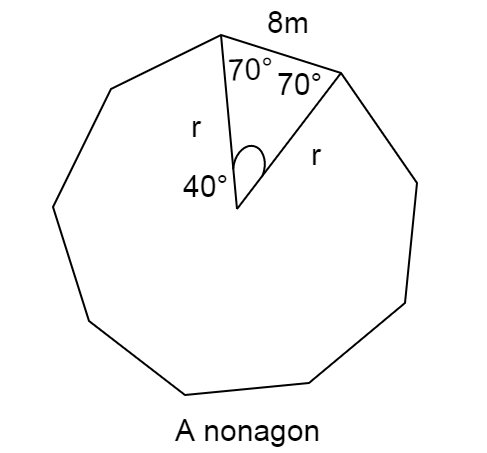
Now by Sine law, we can write
\[ = \dfrac{r}{{\sin 70^\circ }} = \dfrac{8}{{\sin 40^\circ }} = \dfrac{r}{{\sin 70^\circ }}\]
Therefore,
\[ = r = \dfrac{{\sin 70^\circ }}{{\sin 40^\circ }} \times 8\]
Now the area of each isosceles triangle can be obtained by the formula
\[ = \dfrac{1}{2}{r^2}\sin 40^\circ \]
Therefore, the total area of the nonagon is given by
\[ = 9 \times \dfrac{1}{2}{r^2}\sin 40^\circ \]
Putting the value of \[r\] , we get
\[ = 9 \times \dfrac{1}{2}{\left( {\dfrac{{\sin 70^\circ }}{{\sin 40^\circ }} \times 8} \right)^2}\sin 40^\circ \]
On solving, that gives
\[ = 9 \times \dfrac{1}{2} \cdot \dfrac{{{{\sin }^2}70^\circ }}{{{{\sin }^2}40^\circ }} \times 64 \times \sin 40^\circ \]
Or,
\[ = 9 \times 32 \times \dfrac{{{{\sin }^2}70^\circ }}{{\sin 40^\circ }}\]
Putting the values of \[\sin 40^\circ = 0.642\] and \[\sin 70^\circ = 0.939\] we get
\[ = 288 \times \dfrac{{{{\left( {0.939} \right)}^2}}}{{0.642}}\]
That gives,
\[ = 288 \times \dfrac{{0.881}}{{0.642}}\]
Or,
\[ = 288 \times 1.37\]
Hence\[ = 395.214{m^2}\]
Therefore, the area of the nonagon is \[395.214{m^2}\] .

Note: Since we obtained each side of the nonagon, now we can also obtain each interior angle of the nonagon using the formula of sum of all interior angles of a n-sided polygon which is given as,
\[ = \left( {n - 2} \right) \times 180^\circ \] where \[n\] is the number of sides of the polygon.
For a nonagon, \[n = 9\]
Therefore, sum of all interior angles of a nonagon is given by
\[ = \left( {9 - 2} \right) \times 180^\circ \]
i.e.
\[ = 7 \times 180^\circ \]
Hence,
\[ = 1260^\circ \]
Therefore each angle of a nonagon is
\[ = \dfrac{{1260^\circ }}{9}\]
i.e.
\[ = 140^\circ \]
Therefore each angle of a nonagon is \[140^\circ \] .