Question

The perimeter of one face of a cube is 24cm. Find the volume of the cube (in $c{{m}^{3}}$)

Answer 1

Hint: In this question, we are given the perimeter of one face of a cube and we need to find the volume of the cube. As we know, every face of a cube is a square so we are given a perimeter of the square. Using the formula of perimeter of square given by $P=4s$ where s is the side of the square, we will find the side of the square. This side will be the edge of the cube. Hence, we will then apply the formula of volume of cube given by $V={{s}^{3}}$ to find the required volume.

Complete step by step answer:
Here we are given a cube whose perimeter of one face is 24cm. Let us represent it through a diagram where s is the edge of the cube.

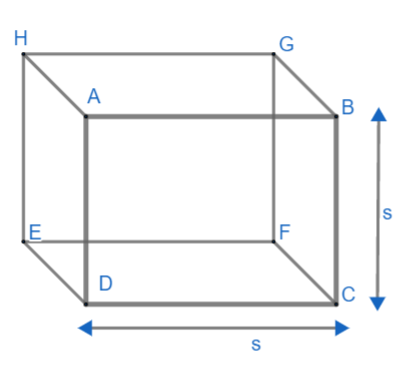
As we can see, one face of the cube is in the shape of the square. Hence, we are given the perimeter of the square ABCD as 24cm. Here, s will represent the side of the square. We know that the perimeter of the square is given by $P=4s$ where s is the side of the cube. So putting the value of perimeter we get: $24=4s$.
Dividing both sides by 4, we get: $s=\dfrac{24}{4}=6cm$.
Hence, the side of the square is 6cm which is also the edge of the cube.
We need to find the volume of the cube.
As we know, the volume of any cube with side s is given by $V={{s}^{3}}$ so putting s = 6cm we get:
$V={{\left( 6cm \right)}^{3}}=6\times 6\times 6c{{m}^{3}}=216c{{m}^{3}}$.

Hence the volume of the cube is $216c{{m}^{3}}$.

Note: Students should always take care of the units while solving these sums. Area is represented by squared units and the volume is represented by cubic units. Since the perimeter was given in cm. So a cubic unit of cm which is $c{{m}^{3}}$ is used for volume. Always try to draw diagrams for better understanding.