Question

The perpendicular distance of the point $P\left(3,4\right)$ from the y-axis is
A.$3$
B.$4$
C.$5$
D.$7$

Answer 1

Hint: In order to find the distance between the point P and the y-axis, initiate with marking the point on the graph, then draw the perpendicular line joining the point P and the point on the y-axis. Either calculate the units or calculate the x-axis distance parallelly to the perpendicular line and will get the results.

Complete step-by-step answer:
We are given with a point $P\left(3,4\right)$. Marking the point on the graph by marking first the point the 3 units in the x-axis and 4 units in the y-axis. Combining them and marking the point. And, the desired representation is:

Now, joining the perpendicular line from the point P to the y-axis, and we get:

Now, drawing a line parallel to this perpendicular in the x-axis from the origin to the same point marked that is 3. And, the figure obtained is as:

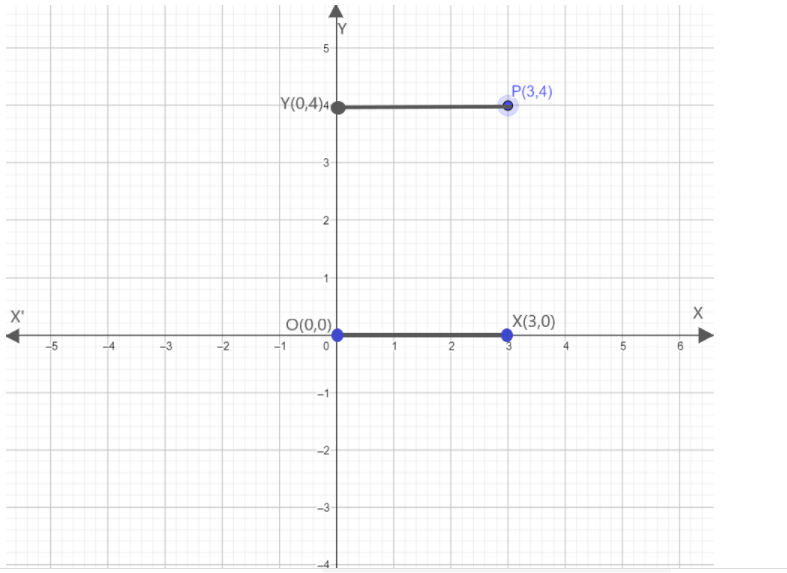
Now, from the graph obtained we can see that the two parallel lines are equal and the length of the parallel will be 3 units as calculating the units from $O\left(0,0\right)$ to $X\left(3,0\right)$.
That means the value of another line that is the from the point perpendicular to the y-axis will also be 3 units.
Hence, the perpendicular distance of the point $P\left(3,4\right)$ from the y-axis is $3$.
Therefore, Option A is correct.
So, the correct answer is “Option A”.

Note: Remember, the perpendicular distance from a point to the y-axis will always be equal to the x-coordinate and the perpendicular distance from a point to the x-axis will always be equal to the y-coordinate.
Despite knowing the fact, it is needed to draw the graph for better understanding.