Question

The picture shows the shape of a boiler. The total height of the boiler is $12m$ and the diameter is 6 meters, the height of the cylindrical part is 6 meters too.
a. What is the height of the cone?

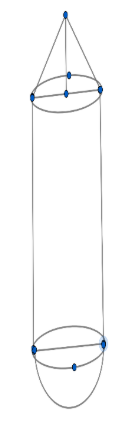
b. How many liters can the boiler hold? ($1{{m}^{3}}=1000litre$)

Answer 1

Hint: To find the height of the cone, subtract the height of the cylinder and radius of the hemisphere from the total height of the boiler. To find how many liters the boiler can hold, add all the volumes, that is the volume of a cylinder, the volume of the hemisphere, and the volume of the cone.


So it is given in the question that the total height of the boiler $=12m$

So the diameter of the cylindrical part $= 6m$.
Also the diameter of the hemispherical part $= 6m$.
So, we can say that, Diameter of cylindrical part $=$ Diameter of the hemispherical part $=6m$.
Also the height of the cylindrical part $=h=6m$.

So it is mentioned in the question that we have to find the height of the cone and how many liters the boiler can hold.

So now, first, we have to find the height of the cone.

For the height of the cone, we can see in the diagram that for calculating the height of the cone we need to subtract the height of the cylinder and radius of the hemisphere from the total height of the boiler.

So Height of cone$=$ Total height of boiler$-$ height of cylinder $-$radius of the hemisphere

So we have a height of cylinder $6m$, and radius of the hemisphere which is half of the diameter i.e.$3m$.

So Height of cone$=12-6-3=3m=H$.
Hence, we get the height of the cone as $3m$.

So now we have to find how many liters the boiler can hold.

So to find how many liters the boiler can hold, we have to find the volume of the boiler.

So for that, we have to consider all the volumes, i.e. volume of a cylinder, the volume of the hemisphere, and volume of a cone.

So the volume of a cylinder$=\pi {{r}^{2}}h$.
The volume of the hemisphere$=\dfrac{2}{3}\pi {{r}^{3}}$.
The volume of a cone$=\dfrac{1}{3}\pi {{r}^{2}}H$.
where $r=$ the radius of cylinder= radius of hemisphere= radius of cone and $h=$ height of the cylinder.

So Volume of boiler $=$ volume of cylinder$+$ volume of hemisphere$+$ volume of a cone.

So we know all the values are mentioned above. Hence, substituting the values we get that,

the volume of the boiler$=\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}+\dfrac{1}{3}\pi {{r}^{2}}H$.


The volume of the boiler$=\dfrac{1}{3}\pi {{r}^{2}}(3h+2r+H)$.
$=\dfrac{1}{3}\pi \times {{3}^{2}}(3\times 6+2\times 3+3)$.
$=\dfrac{\pi \times 9\times 27}{3}$..
$=\dfrac{\pi \times 9\times 27}{3}=254.571{{m}^{3}}$.
It is given that $1{{m}^{3}}=1000$litre.
So the volume of the boiler $=254571$litre.
So we get the height of the cone as $3m$ and volume of the boiler as $254571$litre.

Note: Read the question carefully and solve it accordingly. You should know the volume of a cylinder, the volume of the hemisphere, and also the volume of the cone. So don’t confuse yourself while solving or substituting the values.
Don’t make mistakes while writing the radius or don’t mix up the radius and height of each other. Give a proper name for height and radius.