Question

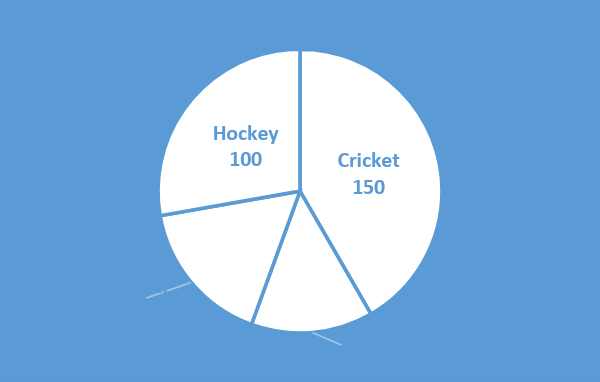
The pie chart shows the amount spent on different sports by a school in a year. The total money spent by the school on sports is Rs1,44,000.
1) What is the maximum spent on cricket?
2) How much more money is spent on hockey than on football?
3) Find the ratio of the amount spent on tennis to that spent on football.
4) What do you think, spending money on sports is justified or is just a waste of money?

Answer 1

Hint:
we will calculate money spent by school on each sport every year from the total amount of money spent on sports. The angle of the sector is given for each sports so we can calculate it by using Money spent on different sports = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$

Formula Used:
As, Total angle of circle is \[360\]
Money spent on different sports = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$

Complete step by step solution:
 Firstly, calculate money spent on hockey, cricket, tennis and football.
Money spent on hockey = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$
\[ \Rightarrow \dfrac{{100 \times 144000}}{{360}}\]
After cancelling all the Zeros from numerator and denominator.
\[ \Rightarrow \dfrac{{10 \times 144000}}{{36}}\]
Multiplying numerator
\[ \Rightarrow \dfrac{{1440000}}{{36}}\]
After Solving we get, \[ \Rightarrow 40000Rs.\]
Money spent on hockey = \[40000Rs.\]
Money spent on cricket = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$
\[ \Rightarrow \dfrac{{150 \times 144000}}{{360}}\]
After cancelling all the Zeros from numerator and denominator.
\[ \Rightarrow \dfrac{{15 \times 144000}}{{36}}\]
Multiplying numerator
\[ \Rightarrow \dfrac{{2160000}}{{36}}\]

After Solving we get, \[ \Rightarrow 60000Rs.\]
Money spent on cricket = \[60000Rs.\]
Money spent on tennis = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$
\[ \Rightarrow \dfrac{{50 \times 144000}}{{360}}\]
After cancelling all the Zeros from numerator and denominator.
\[ \Rightarrow \dfrac{{5 \times 144000}}{{36}}\]
Multiplying numerator
\[ \Rightarrow \dfrac{{720000}}{{36}}\]
After Solving we get, \[ \Rightarrow 20000Rs.\]
Money spent on cricket = \[20000Rs.\]
Money spent on football = $\dfrac{\text{Angle of the sector} \times \text{Total amount spent}}{360}$
\[ \Rightarrow \dfrac{{60 \times 144000}}{{360}}\]
After cancelling all the Zeros from numerator and denominator.
\[ \Rightarrow \dfrac{{6 \times 144000}}{{36}}\]
Multiplying numerator
\[ \Rightarrow \dfrac{{864000}}{{36}}\]
After Solving we get, \[ \Rightarrow 24000Rs.\]
Money spent on cricket = \[24000Rs.\]
(i)As, we calculated the maximum spent on cricket: \[ \Rightarrow 60000Rs.\]
(ii) The money spent on hockey= \[40000Rs.\] and the money spent on football= \[24000Rs.\]
more money is spent on hockey than on football= \[40000Rs.\] \[ - \] \[24000Rs.\]
\[ \Rightarrow 16000Rs.\]
(iii) The money spent on football= \[24000Rs.\]and ) The money spent on tennis= \[20000Rs.\]
The ratio of the amount spent on tennis to that spent on football = $\dfrac{\text{Money spent on tennis}}{\text{Money spent on football}}$
\[ \Rightarrow \dfrac{{20000}}{{24000}}\]
After cancelling all the Zeros from numerator and denominator
\[ \Rightarrow \dfrac{{20}}{{24}}\]
Let’s divide numerator and denominator by 4.
\[ \Rightarrow \dfrac{5}{6}\]
\[Ratio = 5:6\]
(iv) I think spending money on sports is justified as it is a part of our curricular activities as well as it helps in maintaining physical health.

Note:
Remember the total angle of the circle is \[360\] and calculate all the amount of each sport as needed in the question by using the formulas and give the answers accordingly .Do not forget to see the pie chart for the given angles for each sport.