Question

The point of concurrency of the perpendicular bisectors of a triangle is known as
[a] Incentre
[b] Circumcentre
[c] Orthocentre
[d] Centroid.

Answer 1

Hint: For this question recall the definitions of the incentre, the circumcircle, the Orthocentre and the centroid of the triangle. Hence determine which of the options is correct.

Complete step by step solution:
We need to understand the definition of the terms involved in the question.
[1] Incentre: The incentre of a triangle is the centre of the incircle of the triangle.
Consider the figure shown below

Here l is the centre of the incircle. Hence l is the incentre of the triangle.
If we join any vertex with the incentre, the angle corresponding to that vertex will be bisected. Hence incentre is the point of intersection of the angle bisector
[2] Orthocentre: Orthocentre of a triangle is the point of concurrency of the altitudes of the triangle, as shown in the diagram below.

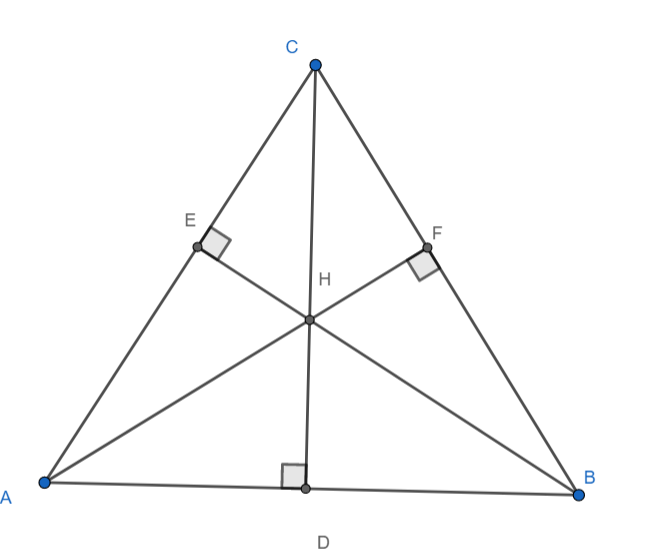
In this diagram H is the point of concurrence of the altitudes of the triangle ABC. H is the Orthocentre of the triangle.
[3] Centroid: Centroid of a triangle is the point of concurrency of the medians of the triangle.

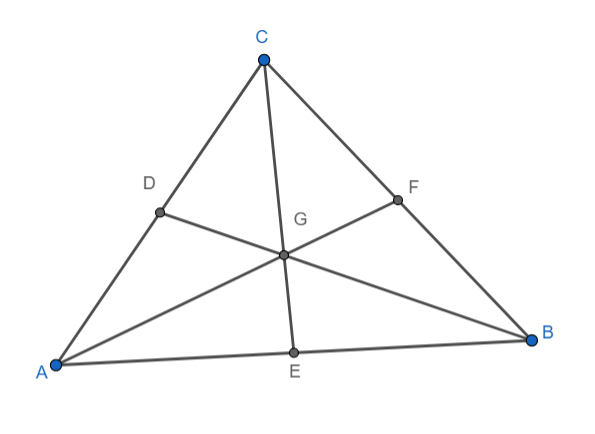
In the diagram below G is the point of concurrency of the medians of the triangle ABC. Hence G is the centroid of the triangle ABC.
[4] Circumcentre: Circumcentre of a triangle is the centre of the circumcircle of the triangle. It is also the point of concurrency of the perpendicular bisector to the sides of the triangle.

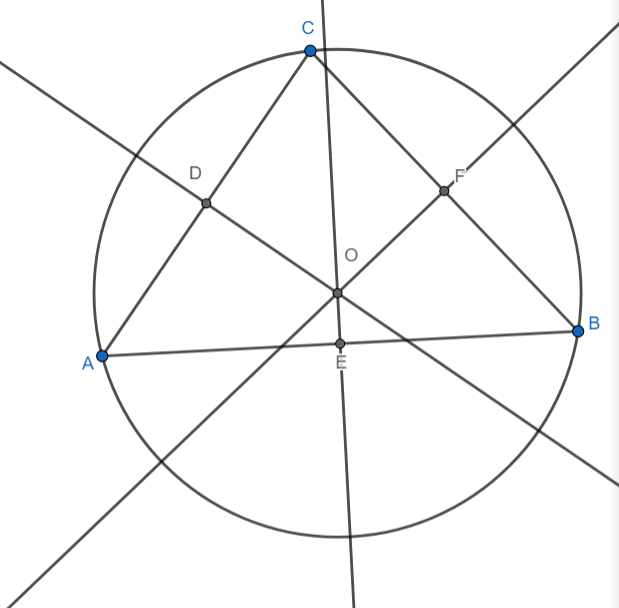
In the diagram above O is the centre of the circumcircle of the triangle ABC. It is also the point of intersection of the perpendiculars. O is the circumcentre of the triangle ABC.
Hence from the above definitions, we conclude that option [b] circumcentre is the correct answer.
Note: In these types of questions, we only need to remember the definitions of various mathematical terms in a triangle. Besides these definitions, the student can memorise the definitions of a nine-point centre, pedal triangle, excentre etc.
Some students do not understand the meaning of concurrency. When three lines intersect each other at a single point, then the three lines are said to be concurrent and the common point of intersection of these lines is known as the point of concurrency.