Question

The points (−1, 0) and (−2, 1) are the two extremities of a diagonal of a parallelogram. If (−6, 5) is the third vertex, then the fourth vertex of the parallelogram is
A) (2, −6)
B) (2, -5)
C) (3, -4)
D) (3, -5)

Answer 1

Hint: We have been given three vertices of parallelogram, extremities of a diagonal are its end points. As the diagonals bisect each other, we can use the coordinates of the midpoint calculated by the given information so as to find the coordinates of the fourth vertex of the parallelogram.
The x coordinate of midpoint is the half of the sum of the x coordinate of the two points whose midpoint it is and same goes for the y coordinate of the midpoint.

Complete step-by-step answer:
We have been given with the three vertices of the parallelogram. Two extremities of diagonals mean these two points will be opposite to each other as they connect the diagonal. The diagram of the parallelogram is given as:

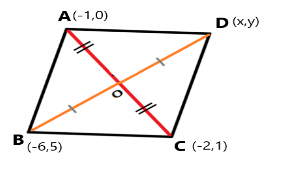
ABCD is a parallelogram. A and C are the extremities of diagonal AC and are on points (−1, 0) and (−2, 1) respectively. The third vertex B has coordinates (−6, 5). Let the coordinates of the fourth vertex D of the parallelogram be (x, y).
In a parallelogram, the two diagonal bisects each other i.e. each diagonal is divided into two equal parts by the other diagonal.
This means that the centre O where both the diagonals intersect becomes the midpoint of both AC and DC.
As O is the midpoint of AC, its respective coordinates will be half the sum of that of points A and C given as:
A = (-1, 0) C = (-2, 1)
Coordinates of O will be
$
  \Rightarrow \left[ {\dfrac{{ - 1 + \left( { - 2} \right)}}{2},\dfrac{{0 + 1}}{2}} \right] \\
  \Rightarrow \left[ {\dfrac{{ - 1 - 2}}{2},\dfrac{1}{2}} \right] \\
  \Rightarrow \left[ {\dfrac{{ - 3}}{2},\dfrac{1}{2}} \right] \\
 $
Thus the coordinates of O are $\left( {\dfrac{{ - 3}}{2},\dfrac{1}{2}} \right)$
Now, O is also the midpoint of BD. So, the half of sum of coordinates of B and D each will be equal to the corresponding coordinate of O.
$\Rightarrow \left( {\dfrac{{x + 6}}{2},\dfrac{{y + 5}}{2}} \right) = \left( {\dfrac{{ - 3}}{2},\dfrac{1}{2}} \right)$
Equating the corresponding coordinates, we get:
$
  \Rightarrow \dfrac{{x - 6}}{2} = \dfrac{{ - 3}}{2} \\
   \Rightarrow x = - 3 + 6 \\
   \Rightarrow x = 3 \\
  \Rightarrow \dfrac{{y + 5}}{2} = \dfrac{1}{2} \\
   \Rightarrow y = 1 - 5 \\
   \Rightarrow y = - 4 \;
 $
The fourth vertex was (x, y), by substituting the values of x and y, we get (3, -4)
Therefore, the fourth vertex of the given parallelogram is (3, -4) and the correct option is C).
So, the correct answer is “Option C”.

Note: Whenever we have any geometrical question related to any quadrilateral or different figures, we first observe which property of that particular figure can be used to obtain the required answer, as in here we use the property of diagonals of a parallelogram.
As the midpoint divides the line joining the two points into equal halves, its respective coordinates are half the sum of the coordinates of the points.