Question

The points A(7,8), B(-5,2) and C(3,6)
A. Are not collinear
B. Cannot be plotted
C. Are not defined
D. Are collinear

Answer 1

Hint: In this problem we have given three points. Now our aim is to find if the given points are collinear or not and the points can be plotted or not defined. To know whether the points are collinear or not we need to find the slope of any two points. So by using the slope formula we precede this problem.

Formula used: Slope of a line $m = \dfrac{{rise}}{{run}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Where, $m = $ slope
$\left( {{x_1},{y_1}} \right) = $ Coordinate of first point in the line
$\left( {{x_2},{y_2}} \right) = $ Coordinate of second point in the line

Complete step-by-step solution:
The given points are $A\left( {{x_1},{y_1}} \right) = \left( {7,8} \right),B\left( {{x_2},{y_2}} \right) = \left( { - 5,2} \right)$ and $C\left( {{x_3},{y_3}} \right) = \left( {3,6} \right)$.
Now suppose three points $A\left( {{x_1},{y_2}} \right),B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ are collinear, then slope of any two points be ${m_{AB}} = {m_{BC}} = {m_{AC}}$
Slope ${m_{AB}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{2 - 8}}{{ - 5 - 7}} = \dfrac{1}{2}$
Slope ${m_{BC}} = \dfrac{{{y_3} - {y_2}}}{{{x_3} - {x_2}}} = \dfrac{{6 - 2}}{{3 + 5}} = \dfrac{1}{2}$ and
Slope ${m_{AC}} = \dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}} = \dfrac{{6 - 8}}{{3 - 7}} = \dfrac{1}{2}$
Therefore, slope of ${m_{AB}} = $Slope of ${m_{BC}} = $Slope of ${m_{AC}}$, that is slope of any two points are same.
Therefore, the given points $A,B$ and $C$ are collinear.
Let us plot the given points in a graph.

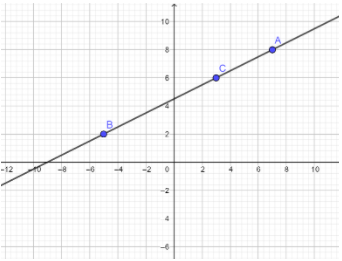
This showed that the points lie on the same line. So the given points are collinear.

Therefore the answer is option (D)

Additional Information: Slope formula method to find that points are collinear. Three or more points are collinear, if the slope of any two pairs of points is the same. With three points $A,B,C$, three pairs of points can be formed, they are $AB,BC,AC$.
If slope of $AB = $ slope of $BC = $ slope of $CA$, then $A$, $B$ and $C$ are collinear.

Note: We can observe that from the problem, suppose the given three points are not collinear then they will not lie on the same line. Slope compares the vertical change (the rise) to the horizontal change (the run) when moving from one fixed point to another along the line. A ratio comparing the change y (the rise) with the change in x (the run) is used to calculate the slope.