Question

The points of a six-pointed star consists of six identical equilateral triangles, with each side 4 cm (see figure). The area of the entire star, including the center, is $m\sqrt 3 $. Find the value of m.

Answer 1

Hint: In this question, we need to determine the value of ‘m’ such that the area of the figure (the star) is $m\sqrt 3 $. For this, we will use the property of the equilateral triangle and the area of the equilateral triangle.

Complete step-by-step answer:
Here, we have to divide the whole figure into a number of the equilateral triangle so that we can calculate the area individually and add them to get the resultant area of the equilateral triangle.

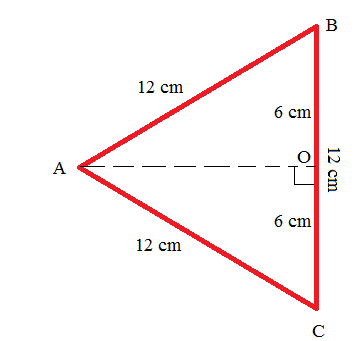
Here, the triangle with the red boundary has 12 cm (4+4+4) length of each side and also, there are three small equilateral triangles with 4 cm of side length.
The area of the given figure is the sum of the area of the equilateral triangle with 12 cm side length and 3 times the area of the equilateral triangle with 4 cm of side length.

The area of the equilateral triangle is $\dfrac{{\sqrt 3 }}{4}$ times the square of the length of the side. Mathematically, $A = \dfrac{{\sqrt 3 }}{4}{a^2}$ where, ‘a’ is the length of the side of the equilateral triangle.
So, the area of the triangle with 12 cm side is given as:
\[
  {A_{12{\text{ cm}}}} = \dfrac{{\sqrt 3 }}{4} \times {\left( {12} \right)^2} \\
   = \dfrac{{\sqrt 3 }}{4} \times 12 \times 12 \\
   = 36\sqrt 3 {\text{ }}{{\text{m}}^2} \\
 \]
Also, the area of the three similar equilateral triangles of side 4 cm is given as:
$
  {A_{4{\text{ cm}}}} = 3 \times \dfrac{{\sqrt 3 }}{4} \times {\left( 4 \right)^2} \\
   = 12\sqrt 3 {\text{ }}{{\text{m}}^2} \\
 $
So, the total area under the given figure is given as:
$
  A = {A_{12{\text{ cm}}}} + {A_{4{\text{ cm}}}} \\
   = 36\sqrt 3 + 12\sqrt 3 \\
   = 48\sqrt 3 {\text{ }}{{\text{m}}^2} \\
 $
Now, comparing the total area calculated with the total area given in the questions to determine the value of the constant ‘m’.
$
  m\sqrt 3 = 48\sqrt 3 \\
  m = 48 \\
 $
Hence, the value of ‘m’ in the expression $m\sqrt 3 $ is 48.
Note: Students should be careful while bifurcating the figure as there are many triangles and shapes in which the figure can be bifurcated. Moreover, the expression for the area of the equilateral triangle should be known to solve the question.