
The position time graph for motion with zero acceleration is:
A.)
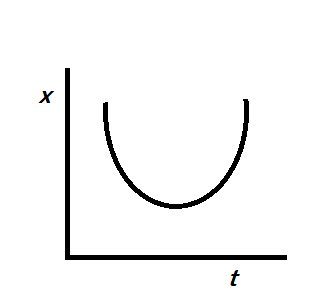
B.)
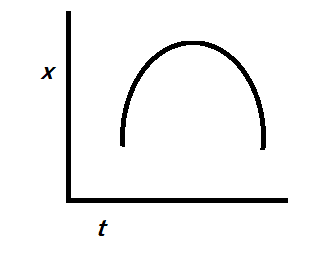
C.)
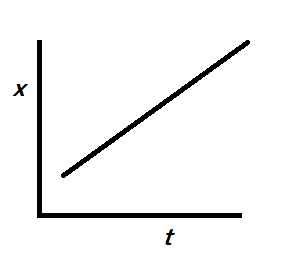
D.)
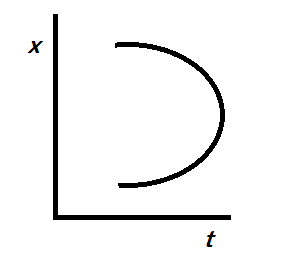
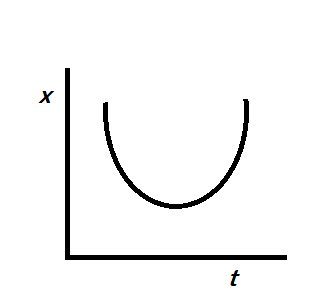
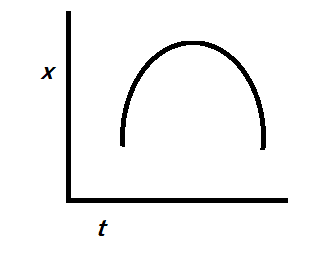
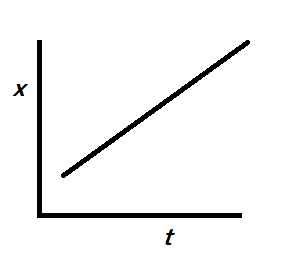
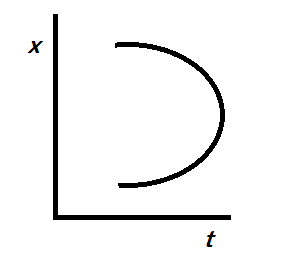
Answer
577.5k+ views
Hint: We know that acceleration is how fast or slow the velocity is with respect to time.This differentiation is nothing but the slope of the graph. Hence we must take the slope of the given curves to find the correct option, among the following.
Formula used:
$a=\dfrac{dv}{dt}=\dfrac{d^{2}x}{dt^{2}}$
Complete answer:
We know that velocity is the rate of change of displacement with respect to time. It is mathematically denoted as $v=\dfrac{dx}{dt}$. This is nothing but the slope of the x-t graph.
Similarly, acceleration is the rate of change of velocity with respect to time. It is mathematically denoted as $a=\dfrac{dv}{dt}$. This is nothing but the slope of the v-t graph.
Given that acceleration is zero, or $a=\dfrac{dv}{dt}=0$, this happens when velocity is a constant . i.e. velocity is independent of time and its slope is $0$.
Since we know from mathematics, that $\dfrac{d}{dx}k=0$
Then the v-t graph is given as:
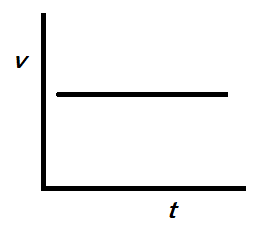
Then for $v$ to be a constant with respect to time we can say that the x-t graph is linear. Like $k\times x$ this is because we know that $\dfrac{d}{dx}kx=k$.
Since the x-t graph must be linear, in the given options, only C is linear and the other options are not linear i.e. specifically quadratic here.
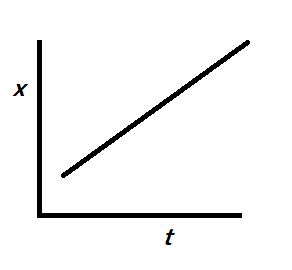
So, the correct answer is “Option C”.
Note:
Here, the answer is discussed in the form of derivation of simplicity. However one can integrate $a=\dfrac{dv}{dt}=0$ twice, to reach the same answer. It is important to know either integration or differentiation to solve this sum. Also note that the slope of the x-t graph is nothing but the velocity and the slope of the v-t graph is the acceleration.
Formula used:
$a=\dfrac{dv}{dt}=\dfrac{d^{2}x}{dt^{2}}$
Complete answer:
We know that velocity is the rate of change of displacement with respect to time. It is mathematically denoted as $v=\dfrac{dx}{dt}$. This is nothing but the slope of the x-t graph.
Similarly, acceleration is the rate of change of velocity with respect to time. It is mathematically denoted as $a=\dfrac{dv}{dt}$. This is nothing but the slope of the v-t graph.
Given that acceleration is zero, or $a=\dfrac{dv}{dt}=0$, this happens when velocity is a constant . i.e. velocity is independent of time and its slope is $0$.
Since we know from mathematics, that $\dfrac{d}{dx}k=0$
Then the v-t graph is given as:
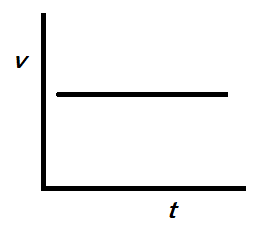
Then for $v$ to be a constant with respect to time we can say that the x-t graph is linear. Like $k\times x$ this is because we know that $\dfrac{d}{dx}kx=k$.
Since the x-t graph must be linear, in the given options, only C is linear and the other options are not linear i.e. specifically quadratic here.
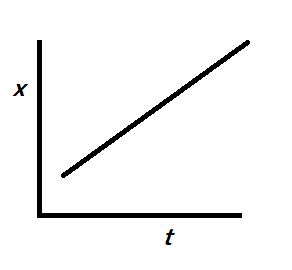
So, the correct answer is “Option C”.
Note:
Here, the answer is discussed in the form of derivation of simplicity. However one can integrate $a=\dfrac{dv}{dt}=0$ twice, to reach the same answer. It is important to know either integration or differentiation to solve this sum. Also note that the slope of the x-t graph is nothing but the velocity and the slope of the v-t graph is the acceleration.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




