Question

The potential energy of a uniform circular disc of radius R and carrying charge density $\sigma $ is
A. \[\dfrac{2}{3}\dfrac{\pi \sigma _{{}}^{2}{{R}^{3}}}{\varepsilon_0}\]
B. \[\dfrac{1}{3}\dfrac{\pi \sigma _{{}}^{2}{{R}^{3}}}{\varepsilon_0}\]
C. \[\dfrac{\pi \sigma _{{}}^{2}{{R}^{3}}}{\varepsilon_0}\]
D. Can Not be determined

Answer 1

Hint: While solving this question, try to find out the expression for the potential energy of a disc with unit area. After that integrate that express to find out the potential of the disc with the required radius/area. Electrical potential energy, or Electrostatic potential energy, is a potential energy (measured in joules) that arises from conservative Coulomb forces and is correlated with the configuration of a certain set of point charges within a given device. An object can provide electrical potential energy from two main elements: its own electrical charge and its relative location to other electrically charged objects.
Formula used:
For solving this question, we will be using the formula for the potential energy, i.e
${{U}_{E}}=k\dfrac{{{q}_{1}}{{q}_{2}}}{r}$

Complete answer:
Area of the disc = $\pi {{R}^{2}}$
So, total charge on the disc will be,
$q=\sigma \pi {{R}^{2}}$
Now, let us assume a small area dA

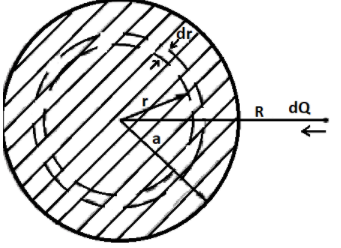
So,
$dA=2\pi rdr$
So, we have
$\begin{align}
  & dq=\sigma dA \\
 & dq=2\sigma \pi rdr \\
\end{align}$
Now,
$\begin{align}
  & dU=\dfrac{kqdq}{r} \\
 & U=\int{dU=\int{\dfrac{kqdq}{r}}} \\
\end{align}$
$\begin{align}
  & \Rightarrow U=2{{\pi }^{2}}K{{\sigma }^{2}}\int\limits_{0}^{R}{{{r}^{2}}dr} \\
 & \Rightarrow U=\dfrac{2{{\pi }^{2}}K{{\sigma }^{2}}{{R}^{3}}}{3} \\
\end{align}$
Now,
Since,
$\Rightarrow K=\dfrac{1}{4\pi {{\varepsilon }_{o}}}$
We have,
$\begin{align}
  & \Rightarrow U=\dfrac{2{{\pi }^{2}}{{\sigma }^{2}}{{R}^{3}}}{3}\dfrac{1}{4\pi {{\varepsilon }_{o}}} \\
 & \Rightarrow U=\dfrac{\pi \sigma _{{}}^{2}{{R}^{3}}}{3{{\varepsilon }_{o}}} \\
\end{align}$
So, the potential energy of a uniform circular disc of radius R and carrying charge density $\sigma $ will be $U=\dfrac{\pi \sigma _{{}}^{2}{{R}^{3}}}{3{{\varepsilon }_{o}}}$.

i.e., Option – C is the correct answer.

Note:
The term "electric potential energy" is used to characterise potential energy in systems with time-variant electrical fields, while the term "electrostatic potential energy" is used to characterise potential energy in systems with time-invariant electrical fields. The term potential energy was invented by the Scottish engineer and physicist William Rankine of the 19th century, although it is related to the Greek philosopher Aristotle 's idea of potentiality.