
The pressure at the bottom of a tank of water is 3P, where P is the atmospheric pressure. If the water is drawn out until the level of water is lowered by one fifth, what is the pressure at the bottom of the tank now?
A.
B.
C.
D.
Answer
496.8k+ views
Hint
The pressure at the bottom of a tank consists of two components. One is the atmospheric pressure and the other is the pressure exerted by the weight of the liquid.
Complete step by step answer
We are provided with the information that the pressure at the bottom of a tank is
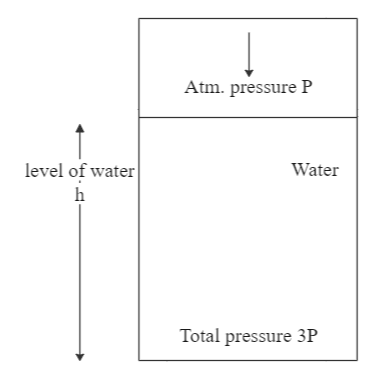
So, if we try to find the pressure exerted by the weight of water in this case, we get:
This gives us the pressure due to the weight of water as
We also know that this pressure can be expressed as:
Now according to the question, we reduce the level of water (i.e. the height of water h) by one fifth. This gives us the new height as:
Solving for
Hence, the new pressure will be given as:
Substituting the value of
We use Eq. 1 to get the answer in generic terms:
Note
The trick here is to check the point at which we need to measure the pressure. For example, the pressure at the top of a tank would only be equal to the atmospheric pressure, but at the bottom it is different (as we saw in this question). The pressure in between is also calculated by the addition of atmospheric pressure and the pressure of the weight of the liquid above that height.
The pressure at the bottom of a tank consists of two components. One is the atmospheric pressure and the other is the pressure exerted by the weight of the liquid.
Complete step by step answer
We are provided with the information that the pressure at the bottom of a tank is

So, if we try to find the pressure exerted by the weight of water in this case, we get:
This gives us the pressure due to the weight of water as
We also know that this pressure can be expressed as:
Now according to the question, we reduce the level of water (i.e. the height of water h) by one fifth. This gives us the new height as:
Solving for
Hence, the new pressure will be given as:
Substituting the value of
We use Eq. 1 to get the answer in generic terms:
Note
The trick here is to check the point at which we need to measure the pressure. For example, the pressure at the top of a tank would only be equal to the atmospheric pressure, but at the bottom it is different (as we saw in this question). The pressure in between is also calculated by the addition of atmospheric pressure and the pressure of the weight of the liquid above that height.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




