Question

The principle of superposition of waves cannot be used to explain wave phenomena such as,
A. Interference
B. Diffraction
C. Stationary waves and beats
D. Dispersion

Answer 1

Hint: The principle of superposition of waves is helpful to calculate the resultant displacement, which has been helpful in interference and diffraction to measure the variation at edges. Stationary waves are developed by the reflection of a wave at a solid surface. Their resultant amplitude can be measured using superposition principle.
Dispersion of waves is a phenomenon which is dependent on behaviour of matter. These all may help you to solve this question.

Complete step by step answer:

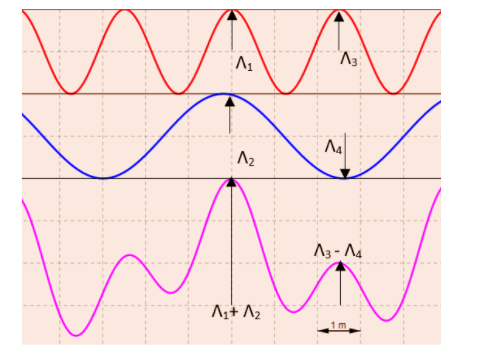
In this figure,
$\lambda_1+\lambda_2$ is the constructive superposition occurring and $\lambda_3-\lambda_4$ is the destructive superposition of the waves.
The principle of superposition can be applied to waves two or more in number which are travelling through similar medium at exact time. The waves can pass through each other without getting disturbed. The resultant displacement of the medium at any point in space or time is defined as the sum of each wave displacement. The phenomenon of interference between the waves is the basis of this concept. If two or more waves traverse the similar space, the resultant amplitude at any point is the sum of the amplitudes of the individual waves. This is also true in diffraction also. Stationary waves are created by the reflection of a wave at a solid surface. Their resultant amplitude can be calculated using superposition principle. The wave dispersion is the phenomenon which depends only on the nature of the wave. Therefore it is not explained using this principle. Hence the correct answer is given as option D.

Note:
In some situations of interference like in noise cancelling headphones, the amplitude of resultant sum of the waves will be smaller than the amplitude variation in its components. This is termed as destructive interference. Opposite to this, in some situations such as in a line array, the resultant amplitude of the variation will be larger than the amplitude of individual waves. This condition is known as constructive interference.