Question

The radii of two circles are 8cms and 6cms respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.

Answer 1

Hint: To solve the given question, we start by finding the area of the given circles from their given radius using the formula of area of circle is equal to $\pi \times {{\left( \text{radius} \right)}^{2}}$. Then we add those areas and equate it to the area of some circle with radius r. By solving it we obtain the radius of the required circle.

Complete step-by-step solution:
Let us consider the radius and area of the first circle as ${{r}_{1}}$ and ${{A}_{1}}$ respectively.
Let us consider the radius and area of the second circle as ${{r}_{2}}$ and ${{A}_{2}}$ respectively.

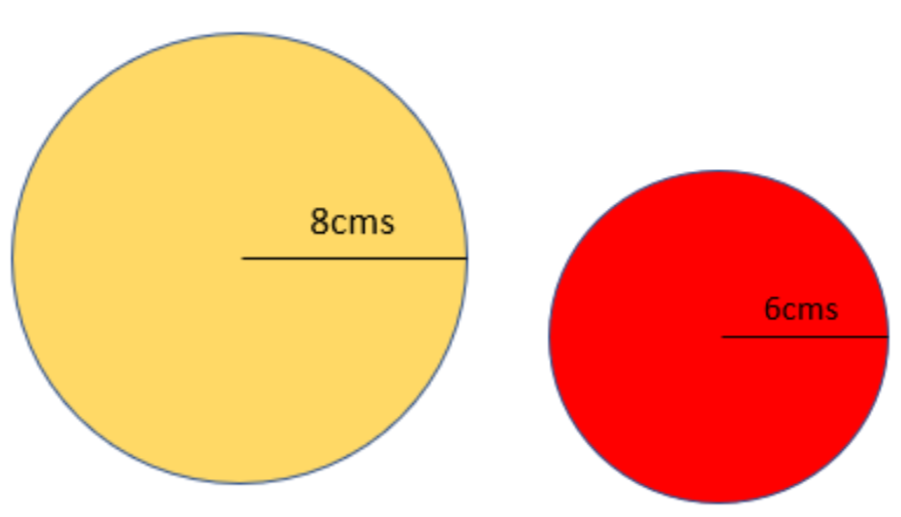
We were given that the radius of the first circle is 8cms, and the radius of the second circle is 6cms.
Given ${{r}_{1}}=8cms$ and ${{r}_{2}}=6cms$.
Using the formula for Area of a circle with radius r.
$Area\text{ }of\text{ }circle=\pi {{r}^{2}}$.
So, let us use the above formula on the first circle and we get area of first circle as,
$\begin{align}
  & \Rightarrow {{A}_{1}}=\pi {{r}_{1}}^{2} \\
 & \Rightarrow {{A}_{1}}=\pi {{\left( 8 \right)}^{2}} \\
 & \Rightarrow {{A}_{1}}=\pi \times 64 \\
 & \Rightarrow {{A}_{1}}=64\pi \ldots \ldots \ldots \left( 1 \right) \\
\end{align}$
So, let us use the above formula again on the second circle and we get area of the second circle as,
$\begin{align}
  & \Rightarrow {{A}_{2}}=\pi {{r}_{2}}^{2} \\
 & \Rightarrow {{A}_{2}}=\pi {{\left( 6 \right)}^{2}} \\
 & \Rightarrow {{A}_{2}}=\pi \times 36 \\
 & \Rightarrow {{A}_{2}}=36\pi \ldots \ldots \ldots \left( 2 \right) \\
\end{align}$
Then the sum of the areas of circles is ${{A}_{1}}+{{A}_{2}}$. So, from equations (1) and (2) we get,
$\begin{align}
  & \Rightarrow {{A}_{1}}+{{A}_{2}}=64\pi +36\pi \\
 & \Rightarrow {{A}_{1}}+{{A}_{2}}=100\pi \ldots \ldots \ldots \left( 3 \right) \\
\end{align}$
We need to find the radius of the circle having its area equal to the sum of areas of the first and second circles.
Let them consider the radius and area of the required circle as $r$ and $A$ respectively.

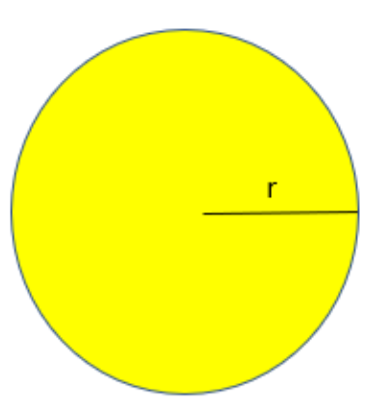
Then by using the formula of area of circle, we get
$A=\pi {{r}^{2}}\ldots \ldots \ldots \left( 4 \right)$
As the sum of the areas of first and second circles is equal to the area of above circle, we get $A={{A}_{1}}+{{A}_{2}}$
So, by using equations (3) and (4)
$\begin{align}
  & \Rightarrow A={{A}_{1}}+{{A}_{2}} \\
 & \Rightarrow \pi {{r}^{2}}=100\pi \\
 & \Rightarrow {{r}^{2}}=100 \\
 & \Rightarrow r=10 \\
\end{align}$
So, the radius of required circle is 10cms.
Hence the answer is 10cms.

Note: One can make a mistake of adding the radii of the circles to find the required radius in the given question. But as the area of the circle is proportional to the square of the radius, we should not add the radius directly to find the radius of the required circle.