Question

The radius of a circle is 5 cm. Find the area of sector formed by the arc of this circle of length 3.5 cm.

Answer 1

Hint: We are given the radius of the circle as 5 cm and the length of the arc is 3.5 cm. If the length of the arc is $l$ cm and radius of circle is $r$cm, then the area of the sector formed is given by $\dfrac{{lr}}{2}$. Substitute the values of $l$ and $r$ to calculate the area of the sector.

Complete step-by-step answer:
Given the radius of the circle is 5 cm.
The arc is the part of the circumference.
The portion formed by an arc of a circle along with its two radii is known as the sector of the circle.

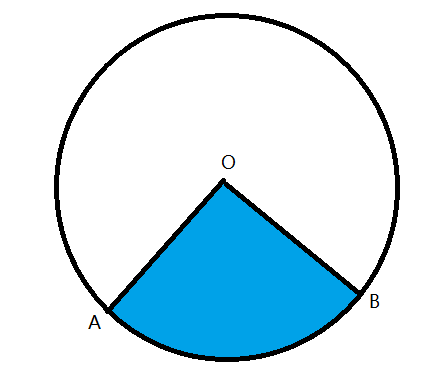
The area of a sector is given by the formula, $\dfrac{{lr}}{2}$, where $l$ is the length of an arc and $r$ is the radius of the circle.
On, substituting the values of $l$ and $r$, we get
$A = \dfrac{{\left( {3.5} \right)\left( 5 \right)}}{2}$
On solving the expression, we get,
$A = \dfrac{{17.5}}{2}$
Thus the area of the sector of length 3.5 cm formed by the circle of radius 5 cm is 8.75 ${\text{c}}{{\text{m}}^2}$.

Note:- The area of the sector of the circle is given by, $\dfrac{{lr}}{2}$ where $l$ is the length of an arc and $r$ is the radius of the circle. If angle between the sector is given, the area of the sector of the circle can also be calculated using the formula, $\dfrac{\theta }{{360}} \times \pi {r^2}$, where $\theta $ is the angle of the sector.