Question

The radius of a circle is increased by 2 cm from 5 cm to 7 cm. Find the increase in area.

Answer 1

Hint: Hint:- We will first write the formula for the area of a circle. Now we will find the areas of both the circle and subtract the area of the circle with radius 5 cm from the area of the circle with 7 cm. Then we will get our answer.

Complete step-by-step answer:
Let us first draw both the circles together, previous one and newer one.

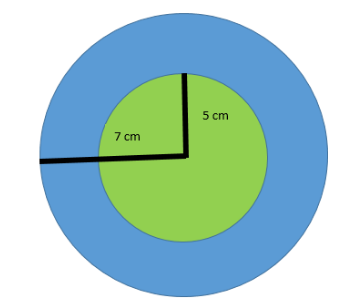
The green circle is the previous one with a radius of 5 cm. The bigger one is the blue circle with 7 cm.
We can clearly see that the area increased will be the blue portion only that is visible to us in the above figure.
To find the area in blue, we will have to find the area of the smaller circle to be subtracted from the area of the bigger circle.
We know that the area of the circle is given by:- $A = \pi {r^2}$, where r is the radius of the circle.
So, difference in area that means the area that we require will be:-
$A = \pi {r_2}^2 - \pi {r_1}^2$, where ${r_1}$ is the radius of the older circle and ${r_2}$ is the radius of the new circle.
We can write it as:-
$A = \pi ({r_2}^2 - {r_1}^2)$
Now we will use the formula: ${a^2} - {b^2} = (a - b)(a + b)$
So, we will get:- $A = \pi ({r_2} - {r_1})({r_2} + {r_1})$
Now putting in the values as: ${r_2} = 7cm$ and ${r_1} = 5cm$.
We will have with us the following expression:-
$ \Rightarrow A = \dfrac{{22}}{7} \times (7 - 5)({7} + 5)$
Simplifying the RHS to get:-
$ \Rightarrow A = \dfrac{{22}}{7} \times 2 \times 12 = \dfrac{{528}}{7}c{m^2}$

Hence, the answer is $\dfrac{{528}}{7}c{m^2}$.

Note: The students might also calculate the areas of both the circles individually and then apply the subtraction between them to get the answer.
*A circle is the only one sided shape with an area.
*A straight line is a circle with an infinite area.
*Circles have no angles.
*A circle has an infinite amount of lines of symmetry.