Question

The radius of a sphere is $9cm$. Find the height of the right circular cone that can be inscribed in the sphere so that the volume of the cone is maximum.

Answer 1

Hint: Cone is inscribed in the sphere means that the corners of the cone touch the sphere internally. We will first draw a diagram to understand the question easily. We will suppose the height of the cone as $h$ and then calculate the volume of the cone in terms of $h$. For finding maximum volume, we will use the first derivative to find the value of $h$ and then use the second derivative to verify if the given volume is maximum or minimum. We will also use Pythagoras’ theorem and volume of cones which are given below.
Pythagoras’ theorem - ${{\left( Hypotenuse \right)}^{2}}={{\left( Height \right)}^{2}}+{{\left( Base \right)}^{2}}$
Volume of cone - $\dfrac{1}{3}\pi {{r}^{2}}h$ , where $r$ is the radius of the base of cone and $h$ is the height of the cone.

Complete step-by-step solution
Let us first draw the diagram.

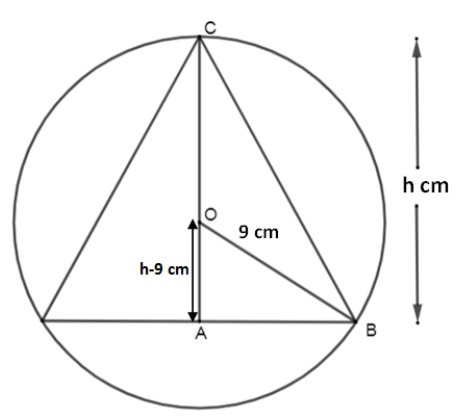
Let the height of the cone be $h$ and the radius of the cone be $r$. From the diagram, we can see that $OAB$ forms a right-angled triangle. Since $OB$ represents the radius of the sphere, therefore $OB=9cm$.
Also, $OC$ represents the radius of the sphere, therefore $OC=9cm$.
As we can see that $AC=h$ and $AC=AO+OC$, therefore
$\begin{align}
  & h=AO+9 \\
 &\Rightarrow AO= h-9 \\
\end{align}$
In right angles triangle $\Delta OAB$, $AO=h-9,BO=9cm$.
Therefore, using Pythagoras’ Theorem,
\[\begin{align}
  & {{\left( BO \right)}^{2}}={{\left( AO \right)}^{2}}+{{\left( AB \right)}^{2}} \\
 &\Rightarrow {{9}^{2}}={{\left( h-9 \right)}^{2}}+{{\left( AB \right)}^{2}} \\
 &\Rightarrow {{\left( AB \right)}^{2}}=81-{{\left( h-9 \right)}^{2}} \\
 & =81-{{h}^{2}}-81+18h \\
 & =18h-{{h}^{2}} \\
\end{align}\]
As we can see $AB$ represents the radius of the base of the cone, therefore \[{{r}^{2}}=18h-{{h}^{2}}\].
Now the volume of the cone is given by –
$V=\dfrac{1}{3}\pi {{r}^{2}}h$, where $r$ is the radius of the base of the cone and $h$ is the height of the cone.
Therefore,
$\begin{align}
 & V=\dfrac{1}{3}\pi \left( 18h-{{h}^{2}} \right)h \\
 &\Rightarrow V=\dfrac{1}{3}\pi \left( 18{{h}^{2}}-{{h}^{3}} \right) \\
\end{align}$
Let us take the derivative of $V$ with respect to $h$. We will get –
$\dfrac{dV}{dh}=\dfrac{1}{3}\pi \left( 36h-3{{h}^{2}} \right)$
Taking $\dfrac{dV}{dh}=0$ will give us two values of $h$, one of them gives maximum volume of cone and the other one gives the minimum volume of the cone.
Therefore,
$\dfrac{1}{3}\pi h\left( 36-3h \right)=0$ gives $h=0$ and $36-3h$ that is $h=12cm$.
Taking derivative of $\dfrac{dV}{dh}$, we get –
$\dfrac{{{d}^{2}}V}{d{{h}^{2}}}=\dfrac{1}{3}\pi \left( 36-6h \right)$
When we put $h=12cm$ in $\dfrac{{{d}^{2}}V}{d{{h}^{2}}}$, we get –
\[\begin{align}
  & {{\left. \dfrac{{{d}^{2}}V}{d{{h}^{2}}} \right|}_{h=12cm}}=\dfrac{1}{3}\pi \left( 36-6\left( 12 \right) \right) \\
 & =-\dfrac{1}{3}\pi 36 \\
 & =-12\pi ,which~is\text{ }negative. \\
\end{align}\]
Therefore, $h=12cm$ represents the maximum volume of cones inscribed in the sphere.


Note: Here, we have taken $h=12cm$ because by second derivative test, we can see that derivative becomes negative at $h=12cm$ so that volume will be maximum at this value of $h$. Take care while finding the radius of the base of the cone and do not get confused between the radius of the sphere and the radius of the base of the cone. Also, we have not taken $h=0cm$ because it will give us zero volume.