Question

The radius of gyration of a solid hemisphere of mass M and radius R about an axis parallel to a diameter \[\dfrac{3}{4}R\] from this plane is given by (Centre of mass of the hemisphere lies at a height \[\dfrac{3R}{8}\] from the base)

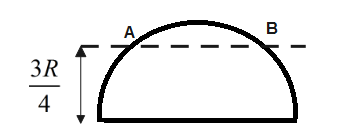
\[\begin{align}
  & A)\dfrac{3R}{\sqrt{10}} \\
 & B)\dfrac{5R}{4} \\
 & C)\dfrac{5R}{5} \\
 & D)\sqrt{\dfrac{2}{5}}R \\
\end{align}\]

Answer 1

Hint: First we have to find the location of centre of mass of the given figure, then we have to apply theorem of parallel axis so that we can find moment of inertia also the centre of mass, then again we apply theorem of parallel axis so that we can find moment of inertia along axis AB. Finally radius of gyration formula is applied and we the required value.

Complete answer:
Since we know that the radius of gyration is the distance of the axis from the centre of mass of the body.
So centre of mass of this figure lies at the middle point on this sphere which is at distance \[\dfrac{3R}{8}\] from the base axis XX’ .Since centre of mass of this given sphere lies at \[\dfrac{3R}{8}\] distance the base. So it is represented by a dotted line passing through the centre of mass and the distance of the centre of mass from axis AB also becomes \[\dfrac{3R}{8}\].

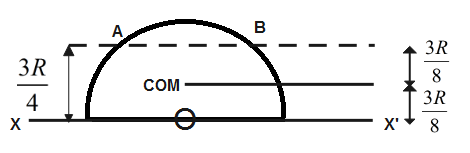
First we have to calculate the Moment of inertia of the solid sphere along the axis passing through the centre of the sphere is given by axis XX’.
\[{{I}_{X{{X}^{'}}}}=\dfrac{2}{5}M{{R}^{2}}\]
Where M be the mass of the solid sphere and R be the radius of the sphere.
Now we find the moment of inertia along the axis passing through the centre of mass by applying the theorem of parallel axis.
\[{{I}_{X{{X}^{'}}}}={{I}_{com}}+M{{(h)}^{2}}\]
Where h is the distance between two parallel axes.
Put the value of h=\[\dfrac{3R}{8}\], we get
\[\Rightarrow \]\[{{I}_{X{{X}^{'}}}}={{I}_{com}}+M{{(\dfrac{3R}{8})}^{2}}\]
\[\Rightarrow \]\[\dfrac{2}{5}M{{R}^{2}}={{I}_{com}}+M\dfrac{9{{R}^{2}}}{64}\]
\[\Rightarrow {{I}_{com}}=\dfrac{2}{5}M{{R}^{2}}-\dfrac{9}{64}M{{R}^{2}}\]
\[\therefore {{I}_{com}}=\dfrac{83}{320}M{{R}^{2}}\] (Equation 1)
Now we find the moment of inertia of axis AB by applying theorem of parallel axis
\[{{I}_{AB}}={{I}_{com}}+M{{({{h}^{'}})}^{2}}\].
Where h’ is the distance between axis of centre of mass and AB axis
Put the value of h’= \[\dfrac{3R}{8}\], we get
\[\Rightarrow {{I}_{AB}}={{I}_{com}}+M{{(\dfrac{3R}{8})}^{2}}\]
Now we put the value of Moment of inertia passing through the centre of mass from equation 1,we get
\[\Rightarrow {{I}_{AB}}=\dfrac{83}{320}M{{R}^{2}}+M{{(\dfrac{3R}{8})}^{2}}\]
\[\Rightarrow {{I}_{AB}}=\dfrac{83}{320}M{{R}^{2}}+\dfrac{9}{64}M{{R}^{2}}\]
\[\Rightarrow {{I}_{AB}}=\dfrac{128}{320}M{{R}^{2}}\]
\[\therefore {{I}_{AB}}=\dfrac{2}{5}M{{R}^{2}}\](Equation 2)
Since for radius of gyration can be represented by :-
\[I=M{{k}^{2}}\]
Applying this relation along the axis AB
\[{{I}_{AB}}=M{{k}^{2}}\](Equation 3)
From equation 2 and 3
\[\Rightarrow \dfrac{2}{5}M{{R}^{2}}=M{{k}^{2}}\]
\[\therefore k=\sqrt{\dfrac{2}{5}}R\].

So the correct option is D.

Note:
With the help of Theorem of parallel axis and theorem of perpendicular axis we can find the moment of inertia along any axis in any figure. Moment of inertia is usually specified with respect to an axis of rotation. It mainly depends also on the distribution of mass around an axis of rotation. For different distributions of mass MOI will change.