Question

The radius of gyration of a solid sphere of radius R about a certain axis is R. The distance of this axis from the centre of the sphere is
A) R
B) $\sqrt {0.5R} $
C) $\sqrt {0.6R} $
D) $\sqrt {0.4R} $

Answer 1

Hint:The radius of gyration and the centre of the square are given to us. We can use these to calculate moment of inertia about the axis of the sphere and the radius of gyration. Then, substituting the values of all the quantities, we can find the required value of the axis (of gyration) from the centre.

Formulas to be used:
$I = m{r^2}$ where I is the moment of inertia, m is the mas of the body and r is the distance from the centre.
${I_B} = {I_C} + {I_R}$, from parallel axes theorem the moment of inertia of the body is equal to the sum of moment of inertia about the centre of the sphere and the about the radius of gyration.
Moment of inertia about the axis of the sphere is $\dfrac{2}{5}m{R^2}$

Complete step by step answer:
The radius of the sphere and radius of gyration, both are given to be equal to R. Then the diagram is given as:

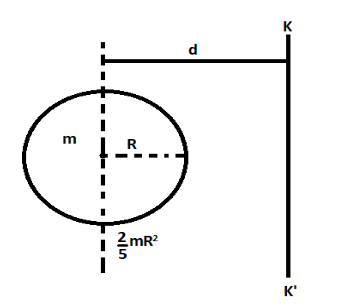
Here,
m is the mas and R is the radius of the sphere. The moment of inertia about the axis of the sphere is $\dfrac{2}{5}m{R^2}$. KK’ is the radius of gyration and the distance between it and the axis of the sphere is d.The axis of the sphere is parallel to the radius of gyration KK’. So we can apply the theorem of parallel axes.
According to the theorem:
The moment of inertia of the body is equal to the sum of moment of inertia about the centre of the sphere and the radius of gyration.
${I_S} = {I_C} + {I_K}$ __________ (1)
Moment of inertia is equal to the product of mass and square of the distance from the centre or axis of rotation. So, the moment of inertias are given as:
${I_s} = m{R^2}$ where m is the mass of the sphere and R is the radius (distance from the centre).
\[{I_C} = \dfrac{2}{5}m{R^2}\] (known value)
${I_K} = m{d^2}$ where m is the mass of the sphere and d is the distance from the centre of the sphere.
Substituting these values in (1), we get:
$m{R^2} = \dfrac{2}{5}m{R^2} + m{d^2}$
Now, we need to calculate the distance between the axes given by d, so calculating for d:
\[
{R^2} = \dfrac{2}{5}{R^2} + {d^2}(m=common) \\
\Rightarrow{d^2} = {R^2} - \dfrac{2}{5}{R^2} \\
\Rightarrow{d^2} = \dfrac{3}{5}{R^2}\left( {LCM} \right) \\
\Rightarrow {d^2} = 0.6{R^2} \\
\Rightarrow \sqrt {{d^2}} = \sqrt {0.6{R^2}} \\
\therefore d = \sqrt {0.6} R \\
\]
Therefore, the distance of the radius of gyration from the centre of the sphere is $\sqrt {0.6R} $ and the correct option is C).

Note:When we measure the distance for calculation of the moment of inertia, it is always measured from the centre of the body. Thus for the sphere, it was its radius and for the radius of gyration, it was the distance between the axes. The radius of gyration is basically an imaginary distance and is generally represented by K.