Question

The radius of gyration of a uniform rod of length l, about an axis passing through a point 1/4 away from the centre of rod, and perpendicular to it, is:
(A) \[\sqrt {\dfrac{7}{{48}}} l\]
(B) \[\sqrt {\dfrac{3}{8}} l\]
(C) \[\dfrac{1}{8}l\]
(D) \[\dfrac{1}{4}l\]

Answer 1

Hint: In order to answer this question, we need to understand that the radius of gyration is defined as the distance between the axis of rotation and the point where the total mass of the body is supposed to be concentrated. So, to find the radius of gyration, we can use the direct formula for the radius of gyration which is dependent on the moment of inertia and mass of the rod. Initially, calculate the moment of inertia using its formula and then substitute it in the formula for radius of gyration. This obtained value will be the radius of gyration of the rod of mass m and length 2l.

Complete step by step solution:
The moment of inertia (MOI) of any uniform rod of length l and mass M about an axis through the centre and forming a 90-degree angle to the length is shown as:
\[{\text{I or moment of inertia = }}\dfrac{{m{l^2}}}{{12}}\]
moment of inertia about c,
\[{I_c} = \dfrac{{m{l^2}}}{{12}}\]

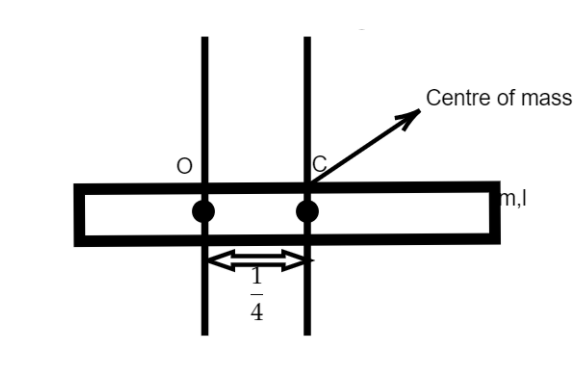
Using Parallel axis theorem:
The parallel axis theorem states that, the moment of inertia of a body about any axis is equal to the moment of inertia about parallel axis through its center of mass plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.
\[{I_o} = {I_c} + \dfrac{{m{l^2}}}{{16}}\]
Substituting the value of \[{I_o}\],
\[ \Rightarrow {I_o} = \dfrac{{m{l^2}}}{{12}} + \dfrac{{m{l^2}}}{{16}}\]
\[ \Rightarrow {I_o} = \dfrac{{4m{l^2} + 3m{l^2}}}{{48}}\]
\[ \Rightarrow {I_o} = \left( {\dfrac{{7m{l^2}}}{{48}}} \right)\]
Let K is the radius of gyration.
\[\therefore {I_o} = m{K^2}\]
\[ \Rightarrow m{K^2} = \left( {\dfrac{{7m{l^2}}}{{48}}} \right)\]
\[ \Rightarrow K = \sqrt {\dfrac{7}{{48}}} {\text{ }}l\]
Hence the correct option is (A).

Note:
It should be remembered that the radius of gyration depends on size and shape of the body. The body mass distribution of the object with respect to the rotational axis also influences the value of radius of gyration. If the body is close to the axis of rotation, then the value for radius of gyration will be less. If the body is away from the axis of rotation, then the value for the radius of gyration will be high. It’s S.I unit is meter.