Question

The ratio of acceleration of pulley to the acceleration of the block is (string is inextensible).

A. $0.5$
B. $2$
C. $1$
D. None of these

Answer 1

Hint: Assume the point on upper string. The velocity of the pulley is the average of the velocity of block and velocity of the point of the string. The point of the string does not move and only the block moves in the direction of force. Differentiate the velocity of the pulley and the block. This is the acceleration of the pulley and block respectively.

Formula used:
Acceleration, \[a = \dfrac{{dv}}{{dt}}\]
Here, v is the velocity and t is the time.

Complete step by step answer:
We assume the velocity of the block is \[{v_b}\] and velocity of the point of the string as shown in the figure below is \[{v_s}\].

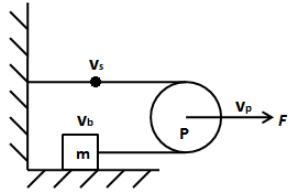
In the above figure, the velocity of the pulley is \[{v_p}\]. We know that the velocity of the pulley is the average of the velocity of block and velocity of the point of the string. Therefore, we can write,
\[{v_p} = \dfrac{{{v_b} + {v_s}}}{2}\]

But we can see that the point of the string does not move and only the block moves by the applied force F. Therefore, the velocity \[{v_s}\] is zero. Thus, we can write the above equation as,
\[{v_p} = \dfrac{{{v_b}}}{2}\] …… (1)
Differentiating the above equation with respect to time, we get,
\[\dfrac{{d{v_p}}}{{dt}} = \dfrac{1}{2}\dfrac{{d{v_b}}}{{dt}}\] …… (2)

But we know that the acceleration is the rate of change of velocity, that is \[a = \dfrac{{dv}}{{dt}}\]. Therefore, we can write the above equation as,
\[{a_P} = \dfrac{{{a_b}}}{2}\]
\[ \therefore \dfrac{{{a_P}}}{{{a_b}}} = 0.5\]
Here, \[{a_P}\] is the acceleration of pulley and \[{a_b}\] is the acceleration of the block. Therefore, the ratio of acceleration of the pulley to the acceleration of the block is 0.5.

So, the correct answer is option A.

Note: Students can directly use the fact that the sum of acceleration of the block and acceleration of the point on the string due to the tension is twice the acceleration of the pulley. Since the string does not move, its acceleration must be zero. Therefore, the acceleration of the block is twice as much as the acceleration of the pulley.