
The reading of a spring balance when a block suspended from it in the air is
A)
B)
C)
D)
Answer
488.4k+ views
Hint:When the block is suspended from the spring balance and completely submerged in water, it experiences an upward thrust exerted by the water which causes the weight of the block to decrease. Specific gravity refers to the ratio of the weight of the block in the air to the change in the weight of the block when it is in water.
Formulas used:
-The change in the weight of a body when it is completely immersed in a liquid is given by,
-The specific gravity of a body is given by,
Complete step by step answer.
Step 1: Sketch a rough figure depicting the block suspended in air and in water and list the readings of the spring balance in the two mediums.
The figure given below describes the block suspended in air and in water.
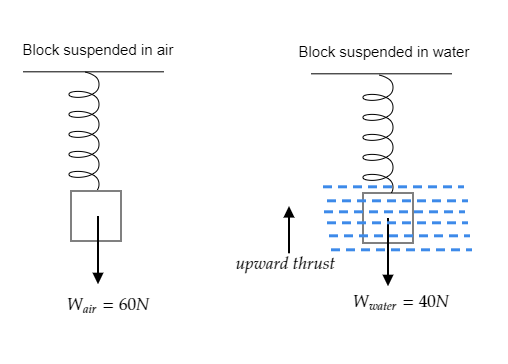
When the block is suspended in air, the spring balance reads
However, when the same block was suspended in water the reading changed to
This is because of the upward thrust acting on the block as shown in the figure.
Step 2: Express the change in weight of the block.
Now the change in weight of the block in the two mediums will be
Substituting for
Thus the change in weight of the block is
Step 3: Express the relation for the specific gravity of the block.
The specific gravity of the given block can be expressed as
Substituting for
Thus we obtain the specific gravity of the block as
So the correct option is A.
Note: Alternate method
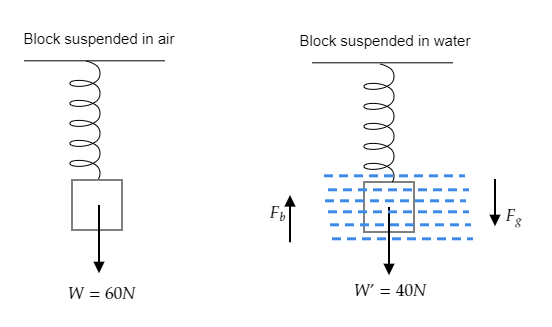
We have the weight of the block in the air as
Archimedes principle gives the upward thrust
Now the force due to gravity is the weight of the block in air and as seen from the figure it is
Then the weight of the block in water will be the sum of the forces acting on it i.e.,
The specific gravity
Substituting equation (A) in (B) we get,
Substituting for
Thus we have the specific gravity of the block as
Formulas used:
-The change in the weight of a body when it is completely immersed in a liquid is given by,
-The specific gravity of a body is given by,
Complete step by step answer.
Step 1: Sketch a rough figure depicting the block suspended in air and in water and list the readings of the spring balance in the two mediums.
The figure given below describes the block suspended in air and in water.

When the block is suspended in air, the spring balance reads
However, when the same block was suspended in water the reading changed to
This is because of the upward thrust acting on the block as shown in the figure.
Step 2: Express the change in weight of the block.
Now the change in weight of the block in the two mediums will be
Substituting for
Thus the change in weight of the block is
Step 3: Express the relation for the specific gravity of the block.
The specific gravity of the given block can be expressed as
Substituting for
Thus we obtain the specific gravity of the block as
So the correct option is A.
Note: Alternate method

We have the weight of the block in the air as
Archimedes principle gives the upward thrust
Now the force due to gravity is the weight of the block in air and as seen from the figure it is
Then the weight of the block in water will be the sum of the forces acting on it i.e.,
The specific gravity
Substituting equation (A) in (B) we get,
Substituting for
Thus we have the specific gravity of the block as
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




