
The relation between T and g is given by
Answer
499.2k+ views
Hint: In the question we are asked to find the relation between ‘T’ and ‘g’. Consider a mass “m” suspended on a wire of length ‘
Formula used:
Time period of a simple oscillation is given by
Complete answer:
To find the relation between ‘T’ and ‘g’,
Let us consider ‘
As we know, time period is given by the equation
Squaring both sides of the equation, we get
From this equation we get,
Thus we can conclude that,
So, the correct answer is “Option D”.
Additional Information:
Time of a simple pendulum derivation:
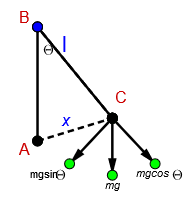
Consider a simple pendulum with a mass ‘m’ suspended on a wire of length ‘
For one oscillation the pendulum is displaced at an angle of ‘
Let
When the pendulum oscillates, it is displaced at a small angle
For this small displacement
Restoring force=
Since the angle of displacement
I.e.
Hence the force here can be rewritten as
Now let us consider the triangle ABC in the figure.
We know that sin of the angle
Here the opposite side of the angle is the displacement ‘x’ and the hypotenuse of the triangle is length ‘
Therefore the restoring force on the pendulum is
By Newton’s second law of motion, we have the equation of motion as
We can rewrite this equation as
From the previous equation, we know that
Eliminating the common terms, we get
For a simple harmonic motion we know that,
On comparing both these equations, we get
By simplifying this,
Time period ‘T’ is given by the equation
Substitute the value of
Therefore time period,
Note:
This question can be solved by another method.
We know that, for a simple pendulum its angular frequency
Time period of an oscillation can also be written as
By substituting the value of angular frequency (
Thus we get
Hence we get the same solution.
Formula used:
Time period of a simple oscillation is given by
Complete answer:
To find the relation between ‘T’ and ‘g’,
Let us consider ‘
As we know, time period is given by the equation
Squaring both sides of the equation, we get
From this equation we get,
Thus we can conclude that,
So, the correct answer is “Option D”.
Additional Information:
Time of a simple pendulum derivation:

Consider a simple pendulum with a mass ‘m’ suspended on a wire of length ‘
For one oscillation the pendulum is displaced at an angle of ‘
Let
When the pendulum oscillates, it is displaced at a small angle
For this small displacement
Restoring force=
Since the angle of displacement
I.e.
Hence the force here can be rewritten as
Now let us consider the triangle ABC in the figure.
We know that sin of the angle
Here the opposite side of the angle is the displacement ‘x’ and the hypotenuse of the triangle is length ‘
Therefore the restoring force on the pendulum is
By Newton’s second law of motion, we have the equation of motion as
We can rewrite this equation as
From the previous equation, we know that
Eliminating the common terms, we get
For a simple harmonic motion we know that,
On comparing both these equations, we get
By simplifying this,
Time period ‘T’ is given by the equation
Substitute the value of
Therefore time period,
Note:
This question can be solved by another method.
We know that, for a simple pendulum its angular frequency
Time period of an oscillation can also be written as
By substituting the value of angular frequency (
Thus we get
Hence we get the same solution.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

The reason why India adopted the policy of nonalignment class 11 social science CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

The plastids which are coloured green and colourless class 11 biology CBSE




